Two coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
(a) 2
(b) 3
(c) 4
(d) 5
The correct Answer is:B
To solve the problem step by step, we need to determine the number of points where maxima are observed when two coherent sources are separated by a distance of 4λ and a detector moves along the x-axis.
Step 1: Understand the setup
- We have two coherent sources S1 and S2 on the y-axis, separated by a distance d=4λ.
- A detector moves along the positive x-axis.
Step 2: Path difference for maxima
- The path difference Δx between the two sources at any point P on the x-axis is given by:
Δx=S1P−S2P
- For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
Step 3: Use the geometry of the setup
- Let S1 be at (0,0) and S2 be at (0,4λ).
- A point P on the x-axis can be represented as (x,0).
- The distances from P to S1 and S2 can be calculated using the Pythagorean theorem:
S1P=√x2+02=x
S2P=√x2+(4λ)2=√x2+16λ2
Step 4: Calculate the path difference
- The path difference is:
Δx=S2P−S1P=√x2+16λ2−x
Step 5: Set up the equation for maxima
- For maxima, we set the path difference equal to nλ:
√x2+16λ2−x=nλ
- Rearranging gives:
√x2+16λ2=nλ+x
- Squaring both sides:
x2+16λ2=(nλ+x)2
- Expanding the right side:
x2+16λ2=n2λ2+2nλx+x2
- Simplifying:
16λ2=n2λ2+2nλx
- Rearranging gives:
2nλx=16λ2−n2λ2
x=16λ−n2λ2n=(16−n2)λ2n
Step 6: Determine valid values of n
- For x to be positive, 16−n2>0 must hold, which gives:
n2<16⟹n<4
- Thus, n can take values 0,1,2,3.
Step 7: Count the maxima
- The values of n that yield maxima are n=0,1,2,3, which gives us a total of 4 maxima.
Final Answer
The number of points where maxima are observed, excluding the origin and far-off points, is 3.
---
- We have two coherent sources S1 and S2 on the y-axis, separated by a distance d=4λ.
- A detector moves along the positive x-axis.
- The path difference Δx between the two sources at any point P on the x-axis is given by:
Δx=S1P−S2P
- For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δx=nλ(n=0,1,2,…)
- Let S1 be at (0,0) and S2 be at (0,4λ).
- A point P on the x-axis can be represented as (x,0).
- The distances from P to S1 and S2 can be calculated using the Pythagorean theorem:
S1P=√x2+02=x
S2P=√x2+(4λ)2=√x2+16λ2
- The path difference is:
Δx=S2P−S1P=√x2+16λ2−x
- For maxima, we set the path difference equal to nλ:
√x2+16λ2−x=nλ
- Rearranging gives:
√x2+16λ2=nλ+x
- Squaring both sides:
x2+16λ2=(nλ+x)2
- Expanding the right side:
x2+16λ2=n2λ2+2nλx+x2
- Simplifying:
16λ2=n2λ2+2nλx
- Rearranging gives:
2nλx=16λ2−n2λ2
x=16λ−n2λ2n=(16−n2)λ2n
- For x to be positive, 16−n2>0 must hold, which gives:
n2<16⟹n<4
- Thus, n can take values 0,1,2,3.
- The values of n that yield maxima are n=0,1,2,3, which gives us a total of 4 maxima.
The number of points where maxima are observed, excluding the origin and far-off points, is 3.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Young'S Double Slit Experiment111videos
WAVE OPTICS
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Polarisation Of Light37videos
WAVE OPTICS
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section D - Chapter End Test30videos
SOURCE AND EFFECT OF MAGNETIC FIELD
Similar Questions
An inteference is observed due to two coherent sources A and B separated by a distance 4λ along Y-axis, where λ is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the total number of maxima observe on the X-axis excluding the points x=0 and x=∞ ?
 View Solution
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View Solution
Knowledge Check
- Question 1 - Select One
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circles - Question 2 - Select One
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpoints - Question 3 - Select One
An interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0, 3l, 0). Here, λ is the wavelength of the sources. Both sources are having equal intensity I0. A detector D is moved along the positive x-axix.

Total number of black points observed by the observer on positive x-axis isAtwoBfourCthreeDfive
Two monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0, 3l, 0). Here, λ is the wavelength of the sources. Both sources are having equal intensity I0. A detector D is moved along the positive x-axix.

Find x-coordinates on the x-axis (exchange x=0 and x=OO).View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
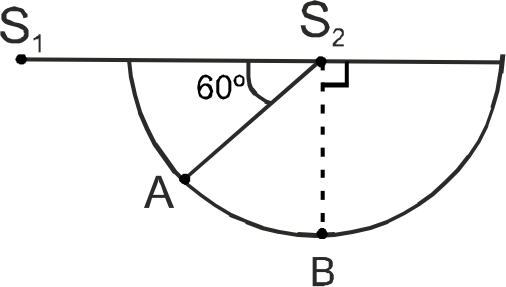
The intensity o sound of B due to S1andS2 is :View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
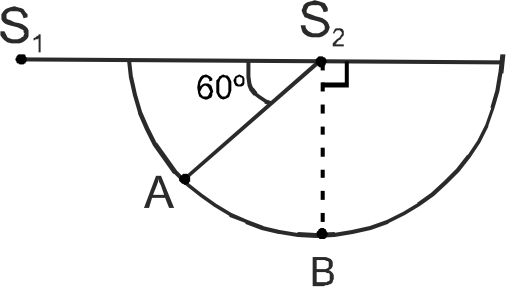
The intensity of sound at A due to S1 only is :View SolutionFigure shows two line sources of sound, S1andS2 separated by a distance 4 m.The two sources are in same phase at all times.The source emit same power and their lengths are also same.A detector moves along a circle with center at S2 and radius 3m. The wavelength of the sound is 1m.When it is at A the intensity of sound due to source S2 only is I0.
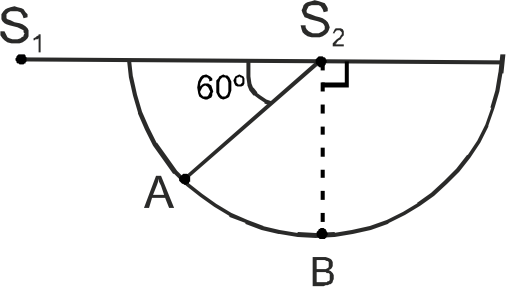
The intensity of sound at B due to S1 only is :View Solution

