The work function of a surface of a photosensitive material is 6.2eV. The wavelength of the incident radiation for which the stopping potential is 5V lies in the
ultraviolet region
visible region
infrared region
X - ray region
The correct Answer is:A
To solve the problem, we need to find the wavelength of the incident radiation using the given work function and stopping potential. We will use the photoelectric equation derived from Einstein's photoelectric effect.
1. Understand the Given Data:
- Work function (Φ) = 6.2 eV
- Stopping potential (V₀) = 5 V
2. Use the Photoelectric Equation:
The energy of the incident photons (E) can be expressed as:
E=eV0+Φ
where e is the charge of an electron (1 eV = 1.6 × 10⁻¹⁹ J).
3. Calculate the Total Energy:
Substitute the values into the equation:
E=(5V)+(6.2eV)=11.2eV
4. Convert Energy to Wavelength:
The energy of a photon is also given by the equation:
E=hcλ
where:
- h (Planck's constant) = 4.1357×10−15eV s
- c (speed of light) = 3×108m/s
Rearranging for wavelength (λ):
λ=hcE
5. Substituting Values:
Substitute h, c, and E into the equation:
λ=(4.1357×10−15eV s)×(3×108m/s)11.2eV
6. Calculate the Wavelength:
λ=1.24071×10−6m eV11.2eV≈1.107×10−7m=110.7nm
7. Determine the Region of Wavelength:
The calculated wavelength of approximately 110.7 nm falls within the ultraviolet (UV) region of the electromagnetic spectrum.
Conclusion:
The wavelength of the incident radiation for which the stopping potential is 5 V lies in the ultraviolet region.
---
- Work function (Φ) = 6.2 eV
- Stopping potential (V₀) = 5 V
The energy of the incident photons (E) can be expressed as:
E=eV0+Φ
where e is the charge of an electron (1 eV = 1.6 × 10⁻¹⁹ J).
Substitute the values into the equation:
E=(5V)+(6.2eV)=11.2eV
The energy of a photon is also given by the equation:
E=hcλ
where:
- h (Planck's constant) = 4.1357×10−15eV s
- c (speed of light) = 3×108m/s
λ=hcE
Substitute h, c, and E into the equation:
λ=(4.1357×10−15eV s)×(3×108m/s)11.2eV
λ=1.24071×10−6m eV11.2eV≈1.107×10−7m=110.7nm
The calculated wavelength of approximately 110.7 nm falls within the ultraviolet (UV) region of the electromagnetic spectrum.
The wavelength of the incident radiation for which the stopping potential is 5 V lies in the ultraviolet region.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - AIIMS Questions
32 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Assertion Reason
14 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section B - Assertion Reasoning
18 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
The work function of a photoelectric material is 4.0 e V. (a) What is the threshold wavelength? (b) find the wavelength of light for which the stopping potential is 2.5 V.
View SolutionWork function of a certain photosensitive mateiral is 2.5 eV. Threshold frequency for the material is ____Hz.
View Solution
Knowledge Check
For a photocell, the work function is ϕ and the stopping potential is Vs . The wavelength of the incident radiation is
AhcϕBhcϕ−eVsChcϕ+eVsDhceϕ+VsThe photoelectric work function of the emitter of a photocell is 3.63 eV . The frequency of incident light radiation if the stopping potential of the emitter is 3 volt , is
A1.1×1015 HzB6.6×1015 HzC1.6×1015 HzD6.1×1015 HzWhich of the following is the graph between the frequency (v) of the incident radiations and the stopping potential ?
A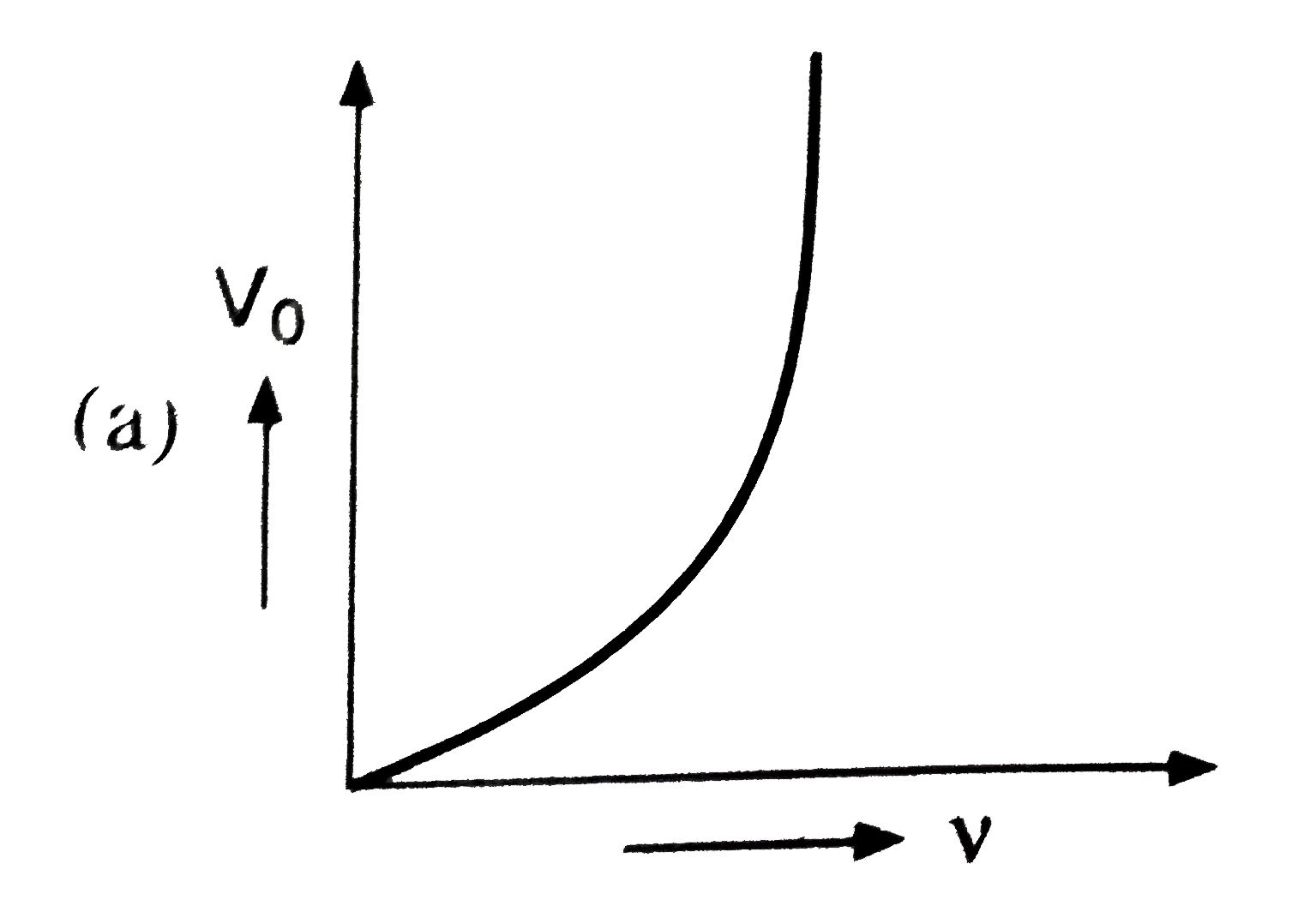 B
B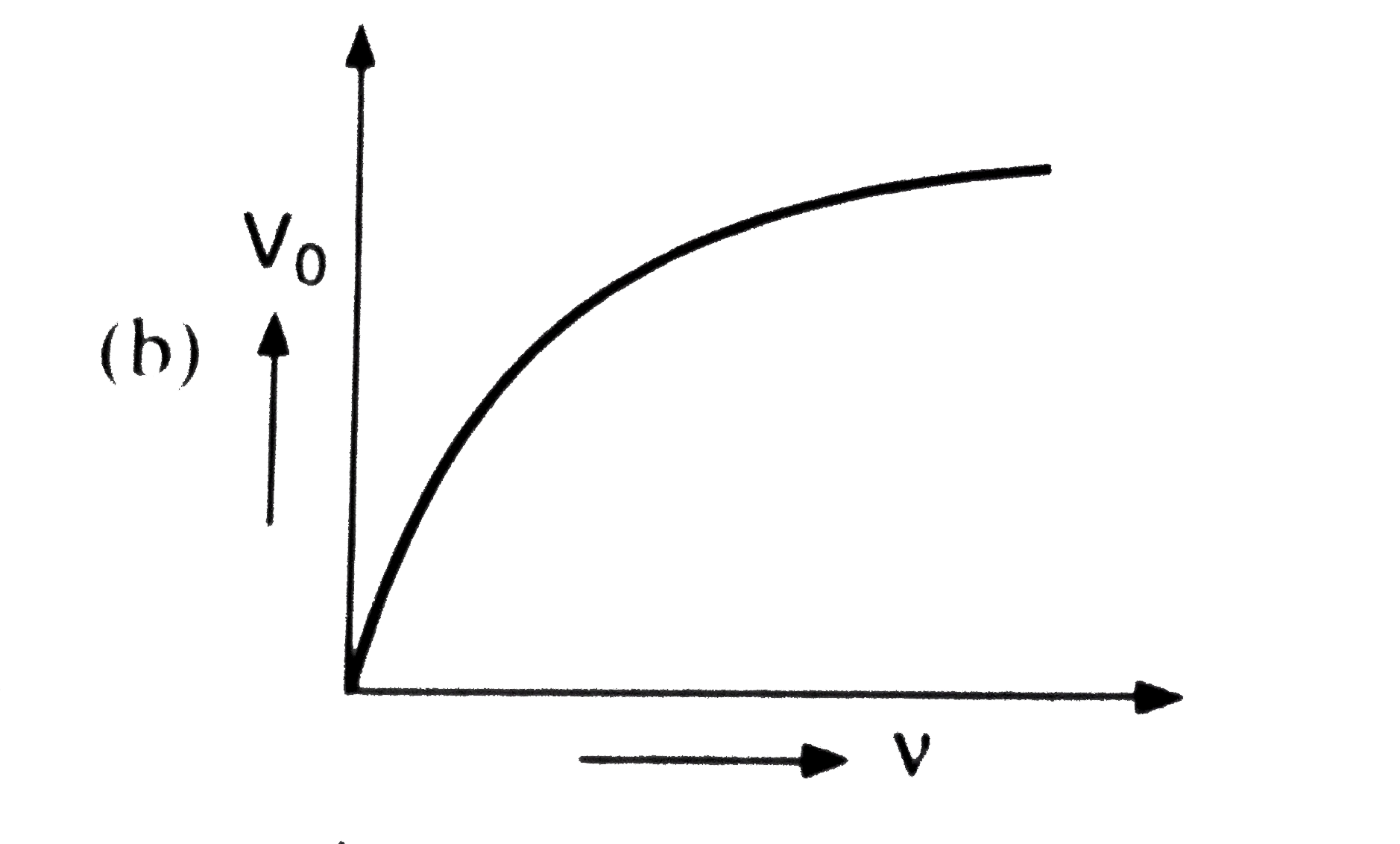 C
C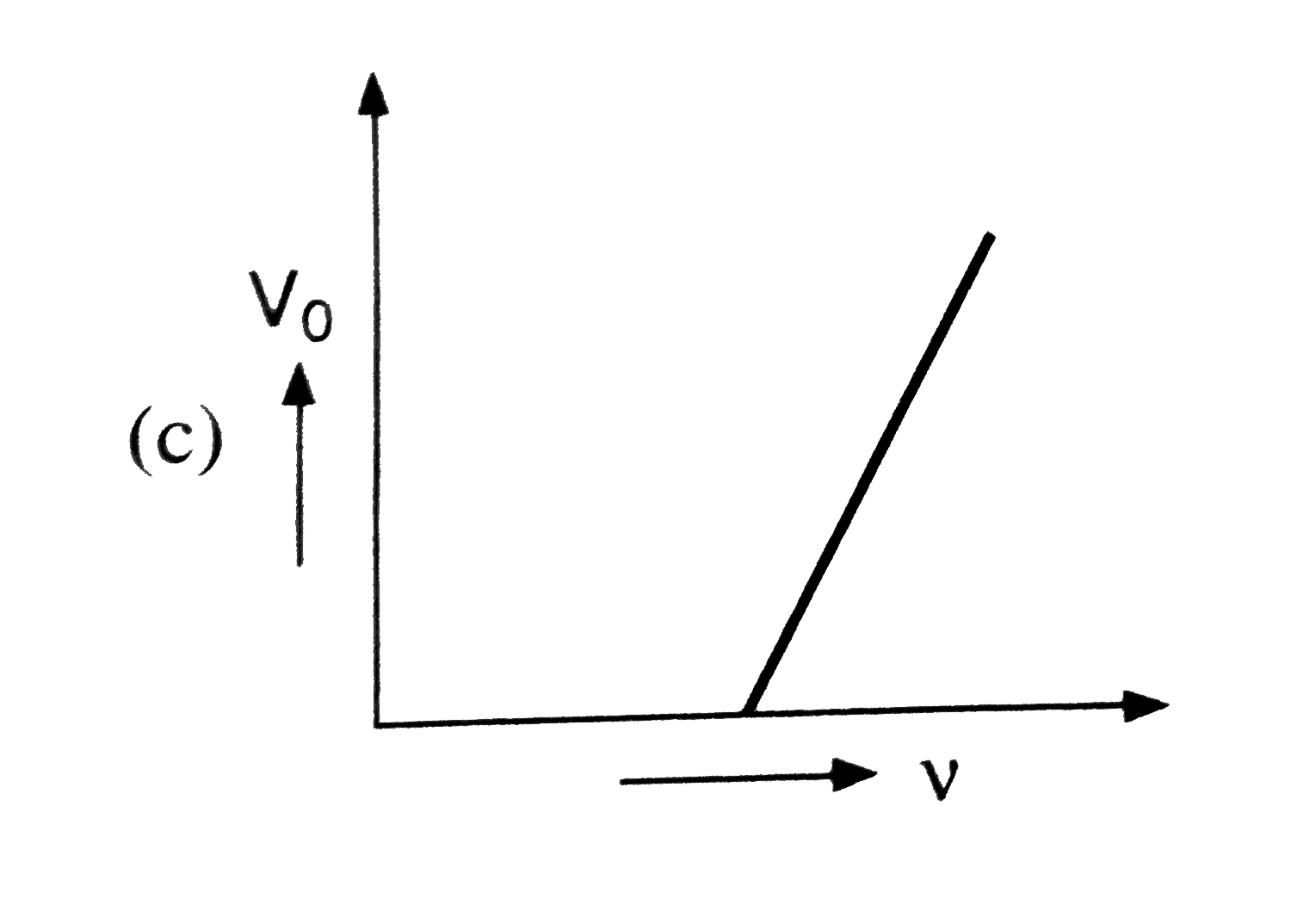 D
D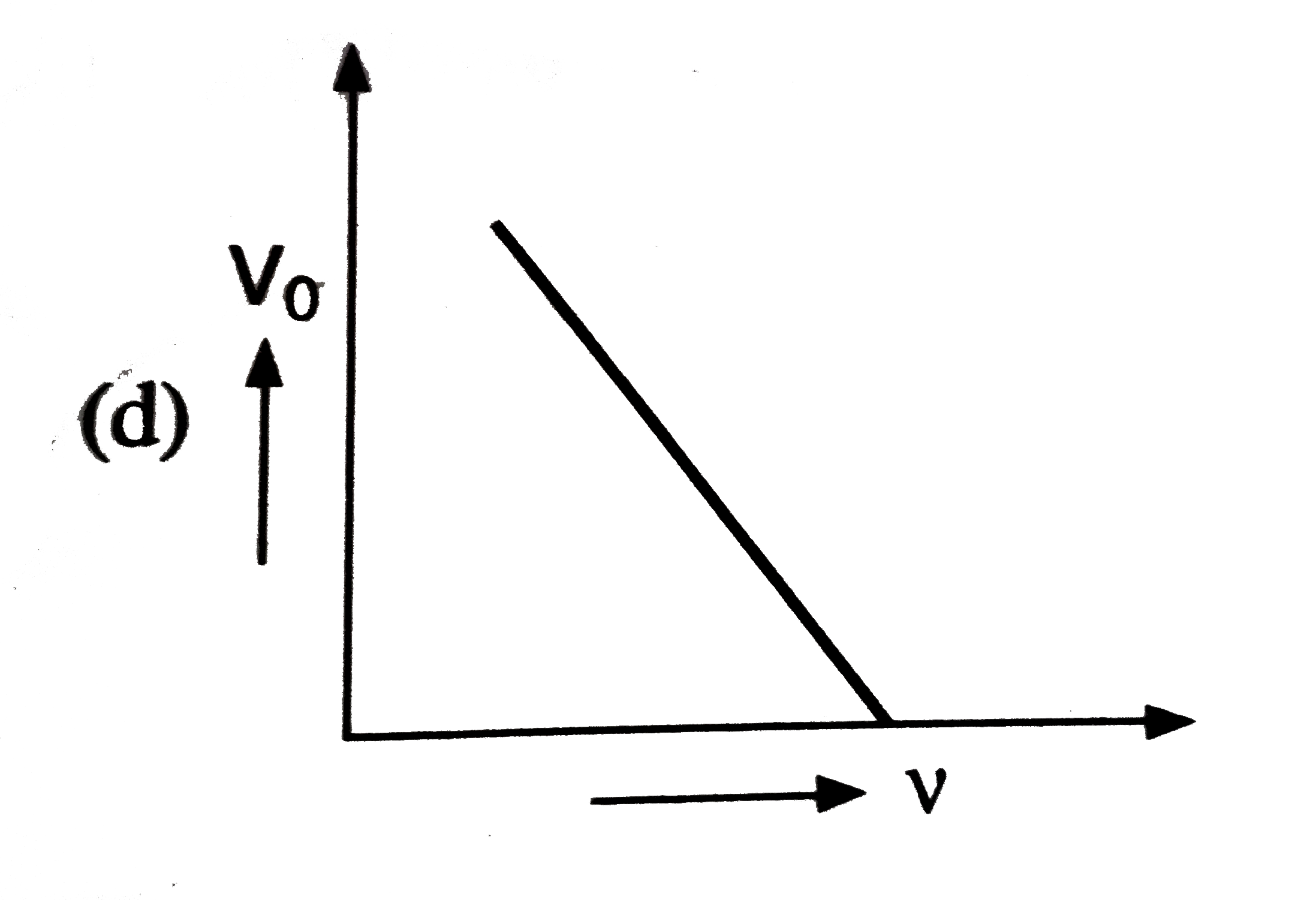
The work function of a material is 4.5eV. What is the maximum wavelength of incident light for which electrons will be emitted?
View SolutionCalculate the velocity of a photo-electron, if the work function of the target material is 1.24 eV and the wavelength of incident light is 4360Å. What retarding potential is necessary to stop the emission of the electrons?
View SolutionLight of 3,000Å is incident on a surface of work function 4 eV .
calculate the wavelength of light to be incident on the surface such that the stopping potential is zero.
View SolutionWhen light off frequency v1 is incident on a photosensitive surface , the stopping potential is V1 . If the frequency of incident radiation becomes v1/2 the stopping potential changes to V2 Find out the expression for the threshold frequency for the surface in terms of V1andV2
If the frequency of incident radiation is doubled , will the maximum kinetic energy of the photoelectrons also be doubled ? Given reason .
View SolutionAn electron of work function 1.4 eV is emitted with a velocity 5×106 m/s . The wavelength of the incident radiation is
View Solution
