In a radio receiver, the short wave and medium wave station are tuned by using the same capacitor but coils of different inductance Ls and Lm respectively then
Ls>Lm
Ls<Lm
Ls=Lm
None of these
The correct Answer is:B
Asv=cλ⇒Vm=cλm and vs=cλs
∴λm>λs⇒vm<vs
Also vm=12π√LmC and vs=12π√LsC
⇒vmvs=√LsLm⇒Ls<Lm
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Problems Based On Mixed Concepts39videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section B - Assertion Reasoning13videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section D - Chapter End Test30videos
GEOMETRICAL OPTICS
Similar Questions
In a radio receiver, the short wave and medium wave station are tuned by using the same capacitor but coils of different inductance Ls and Lm respectively then
View SolutionTwo coils – 1 and 2 – are mounted co axially as shown in the figure. The resistance of the two coils are R1 and R2 and their self inductances are L1 and L2 respectively. Switch S is closed at time t = 0 to connect the coil 1 to an ideal cell of emf V. It is observed that by the time current reaches its steady value in coil 1, the quantity of charge that flows in coil 2 is Q0. Calculate the mutual inductance (M) between the two coils.
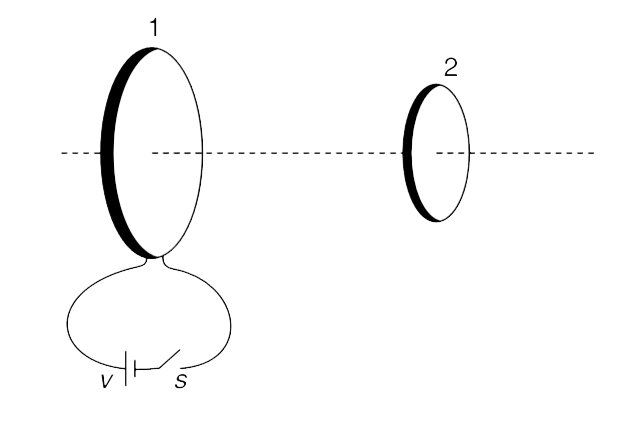 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a radio receiver, the short wave and medium wave station are tuned by using the same capacitor but coils of different inductance Ls and Lm respectively then
ALs>LmBLs<LmCLs=LmDNone of these - Question 2 - Select One
Long distance short - wave radio brad - casting uses
Aground waveBionospheric waveCdirect waveDsky wave - Question 3 - Select One or More
Two different coils have self-inductance L1=8mH,L2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same rate. At a certain instant of time, the power given to the two coils is the same. At that time the current, the induced voltage and the energy stored in the first coil are i1,V1 and W1 respectively. Corresponding values for the second coil at the same instant are i2,V2 and W2 respectively. Then
Ai1i2=14Bi1i2=48CW2W1=4DV2V1=14
Long distance radio broadcasts use short wave bands. Explain why?
View SolutionIt was observed that at a receiving station at Ahmedabad, the longitudinal waves and transverse waves produced during the Gujarat earthquake arrived at speeds of x m/s and y m/s respectively. The two waves are received at an interval of t seconds. Find the distance between the receiving station and Bhuj where the epicentre of the earthquake was located. (x>y)
View SolutionTwo different coils have self-inductances L1=8mHandL2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are i1,V1andW1 respectively. Corresponding values for the second coil at the same instant are i2,V2andW2 respectively. Then:
View SolutionTwo different coils have self inductances L1=9mH and L2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coils is the same. At that time, the current the induced voltage and the energy stored in the first coil are i1,V1 and W1 respectively.
Corresponding values for the second coil at the same instant are i2,V−2 and W2 respectively. Then,View SolutionTwo coils have self-inductance L1=4mH and L2=1mH respectively. The currents in the two coils are increased at the same rate. At a certain instant of time both coils are given the same power. If I1 and I2 are the currents in the two coils, at that instant of time respectively, then the value of (I1/I2) is :
View Solution

