Two coils – 1 and 2 – are mounted co axially as shown in the figure. The resistance of the two coils are R1 and R2 and their self inductances are L1 and L2 respectively. Switch S is closed at time t = 0 to connect the coil 1 to an ideal cell of emf V. It is observed that by the time current reaches its steady value in coil 1, the quantity of charge that flows in coil 2 is Q0. Calculate the mutual inductance (M) between the two coils.
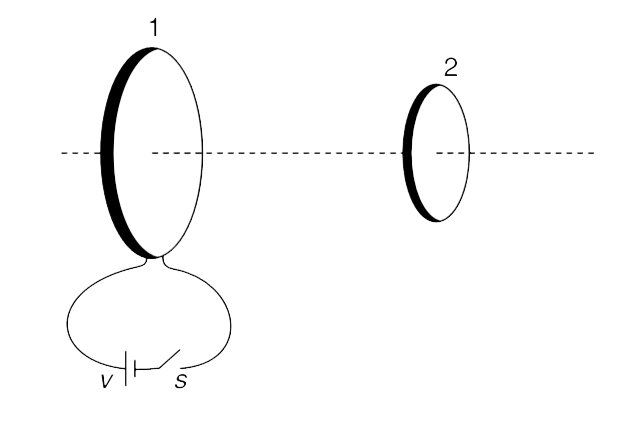
The correct Answer is:R1R2Q0V
Step by step video, text & image solution for Two coils – 1 and 2 – are mounted co axially as shown in the figure. The resistance of the two coils are R_(1) and R_(2) and their self inductances are L_(1) and L_(2) respectively. Switch S is closed at time t = 0 to connect the coil 1 to an ideal cell of emf V. It is observed that by the time current reaches its steady value in coil 1, the quantity of charge that flows in coil 2 is Q_(0). Calculate the mutual inductance (M) between the two coils. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:ARIHANTChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 3
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:ARIHANTChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 3
Explore 12 Videos
- CURRENT ELECTRICITYBook:ARIHANTChapter:CURRENT ELECTRICITYExercise:Current Electricity
Explore 105 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
Similar Questions
A short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
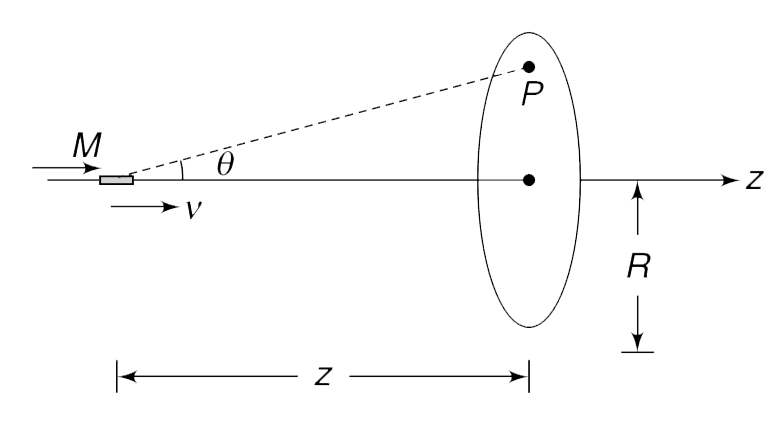
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.

(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
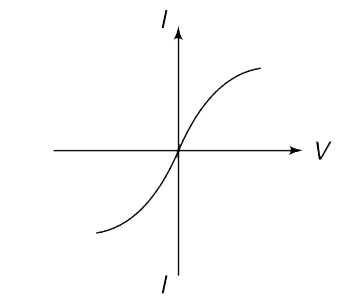
View SolutionThe current-voltage graph for a resistor is as shown in the figure. Is it right to say that resistance decreases as the current through it increases ?
View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionTwo different coils have self-inductances L1=8mHandL2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are i1,V1andW1 respectively. Corresponding values for the second coil at the same instant are i2,V2andW2 respectively. Then:
View SolutionIn the circuit, a battery of emf E, a resistance R and inductance coil L1andL2 and switch S are connected as shown. In Fig. Initially the switch is open
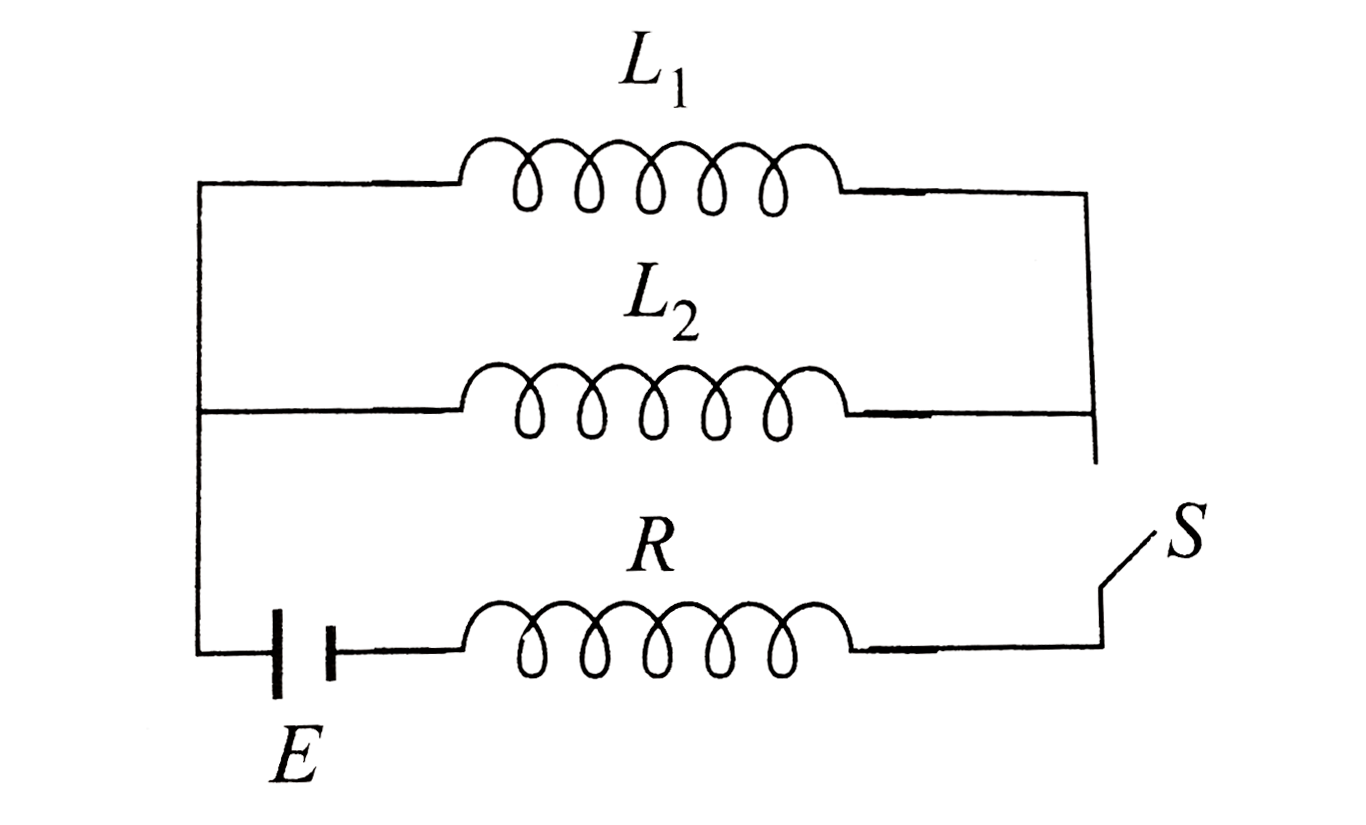
View SolutionAn oscillating circuit consists of two coils connected in series whose inductances are L_(1) and L_(2) active resistances are R_(1) and R_(2) , and mutual inductance is negligible. These coils are to be replaced by one, keeping the frequency and the quality factor of the circuit constant. Find the inductance and the active resistance of such a coil.
View SolutionA wooden core ( figure ) supports two coils : coil 1 with inductance L1 and shor − circuited coil 2 with active resistance R and inductance L2. The mutual inductance of the coils depends on the distance x between them according to the law L12(x). Find the mean ( averaged over time ) value of the interaction force between the coils when coil 1 carries an alternating current I1=I0cosωt
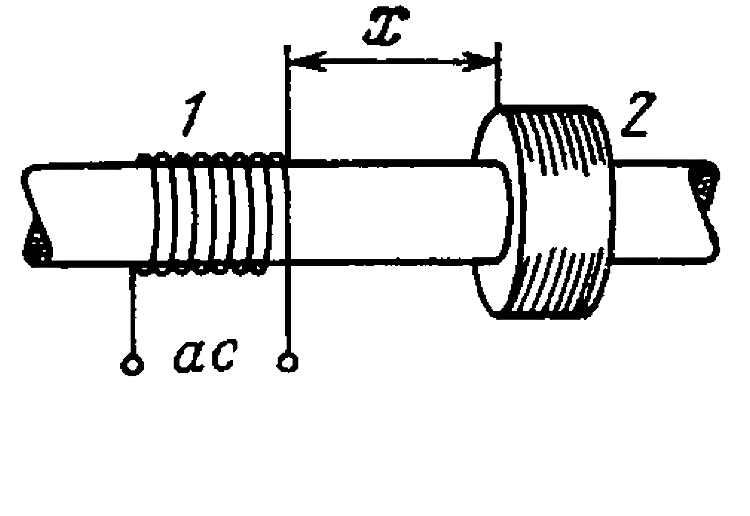
View SolutionTwo coils of self inductance L_(1) and L_(2) are connected by in parllel and the then to cell of emf epsilon and of resistance R throught a Key . Find the instantaneous current throught L after the key is closed .
View SolutionTwo different coils have self inductances L_(1)=8mH and L_(2)=2mH . The current in both the coil is increased at same constant rate. At a certain instant power given to two coils is same. At that time the energy stored in both the coils are V_(1) & V_(2) respectively, then (V_(1))/(V_(2)) is
View SolutionTwo coils of self inductance L_(1) and L_(2) are connected in parallel and then connected to a call of emf epsilon and internal resistance - R. Find the steady state current in the coils.
View Solutionदो कुण्डलियाँ P और S के स्वप्रेरकत्व क्रमशः L1 व L2 हैं। यदि उनके बीच आदर्श फ्लक्स युग्मन है, तो सिद्ध कीजिए की इन कुंडलियों के मध्य अन्योन्य प्रेरकत्व M=√L1L2 होगा।
View SolutionMutual inductance of two coils depends on their self inductance L1 and L2 as :
View Solutionदो आदर्श प्रेरक (ideal inductor ) L1एवं L2 और एक प्रतिरोध (resistance) R को एक अचल वोल्टता के स्रोत से एक स्विच द्वारा जोड़ा जाता है (जैसा चित्र में दिखाया गया है), L1एवं L2 के बीच अन्योन्य प्रेरकत्व (mutual inductance) नहीं है। प्रारम्भ में स्विच खुला है। समय 1 = 0 पर स्विच बन्द किया जाता है और धारा बहनी शुरू होती है। निम्न में कौन-सा/से प्रकथन सही है/हैं?
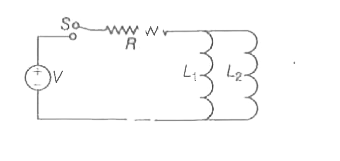
View SolutionTwo different coils have self-inductances L1=8mHandL2=2mH. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are i1,V1andW1 respectively. Corresponding values for the second coil at the same instant are i2,V2andW2 respectively. Then:
View Solution