ψ2 ,( psi) the wave function resperesents the probability of finding electron . Its value depends :
How much it is inside the nucleus
How much it is far from the the nuycleus
How much it is near the nucleus
Upon the type of orbital
The correct Answer is:D
For s-orbitals, ψ2 is maxumum for closer to nucleus . For p-bitals ψ2 maximum for fa away distance from nucleus .
Topper's Solved these Questions
- BOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 3B19videos
ATOMIC STRUCTURE
- BOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 439videos
ATOMIC STRUCTURE
- BOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise19videos
ATOMIC STRUCTURE
- BOOK - P BAHADURCHAPTER - CHEMICAL BONDINGEXERCISE - Exercise 711videos
CHEMICAL BONDING
Similar Questions
ψ2 determine the probability of finding the electron in particular region of sapce
View Solution24.Choose the correct statements from the following - A) A node is a point in space where the wave function ( Ψ ) has zero amplitude B) Total number of nodes in an orbital is equal to (n-1) C) Ψ2 represents the probability density of finding the electron D) Total no.of angular node in 2px orbital is one
View Solution
Knowledge Check
- Question 1 - Select One
Assertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical
Reason. Probability density is Ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.AIf both assertion and reason are true, and reason is the true explanation of the assertionBIf both assertion and reason are true, but reason is not the true explanation of the assertionCIf assertion is true, but reason is falseDIf both assertion and reason are false - Question 2 - Select One
Assertion(A): ψ indicates the amplitude of electron-wave
ψ2 denotes probability of finding an electron in the space around the nucleusABoth (A) and (R) are true and (R) is the correct explanation of (A)BBoth (A) and (R) are true and (R) is not the correct explanation of (A)C(A) is true but (R) is falseD(A) is false but (R) is true - Question 3 - Select One
Probability of finding the electron ψ2 of 's' orbital does not depend upon
Adistance from the nucleus (r)Benergy of 's' orbitalCprincipal quantum numberDazimuthal quantum number
Choose the correct statements from the following - A) A node is a point in space where the wave function (Ψ) has zero amplitude B) Total number of nodes in an orbital is equal to (n-1). C) Ψ2 represents the probability density of finding the electron D) Total no.of angular node in 2px orbital is one
View SolutionChoose the correct statements from the following:
(A) A node is a point in space where the wave function Ψ has zero amplitude.
(B) Total number of nodes in an orbital is equal to (n−1)
(C) Ψ2 represents the probability density of finding the electron
(D) Total no.of angular node in 2px orbital is oneView SolutionOrbitals are the pictorial representationofΨ or Ψ2

Ψ2 tell about the probability of finding electron.
Which of the following graph is correct for 3p ?View SolutionOrbitals are the pictorial representationofΨ or Ψ2
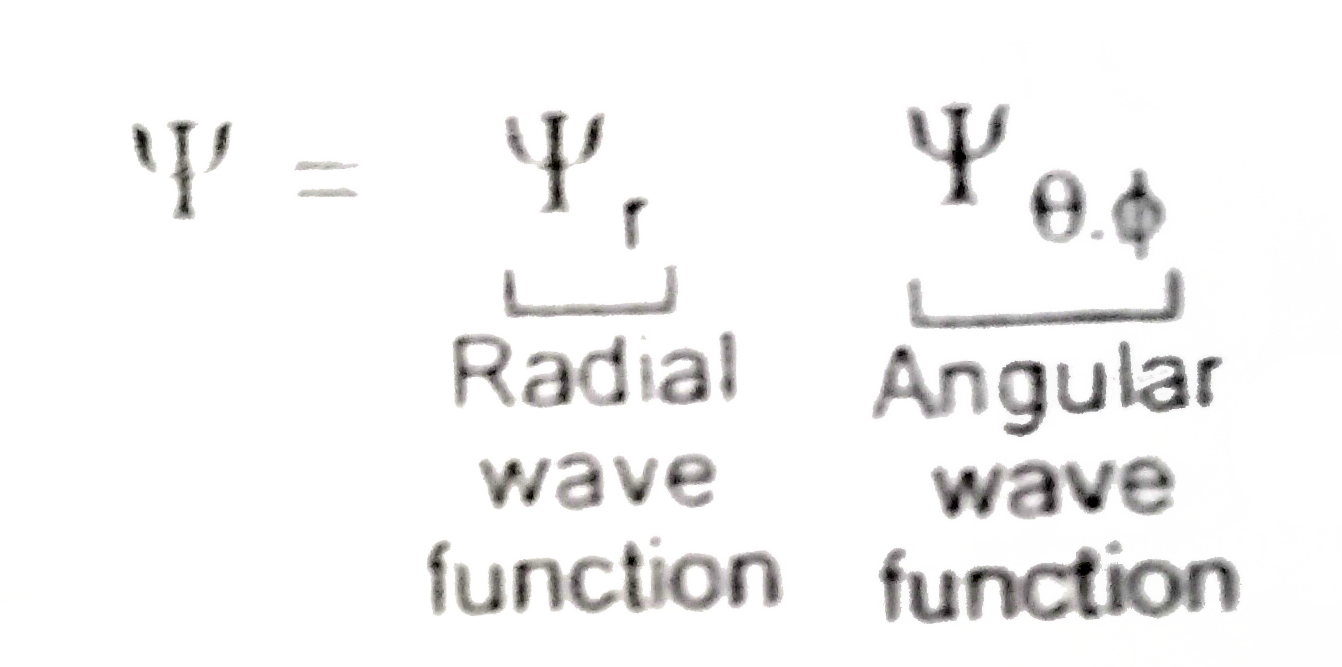
Ψ2 tell about the probability of finding electron.
A 2px orbital is shown by given diagram
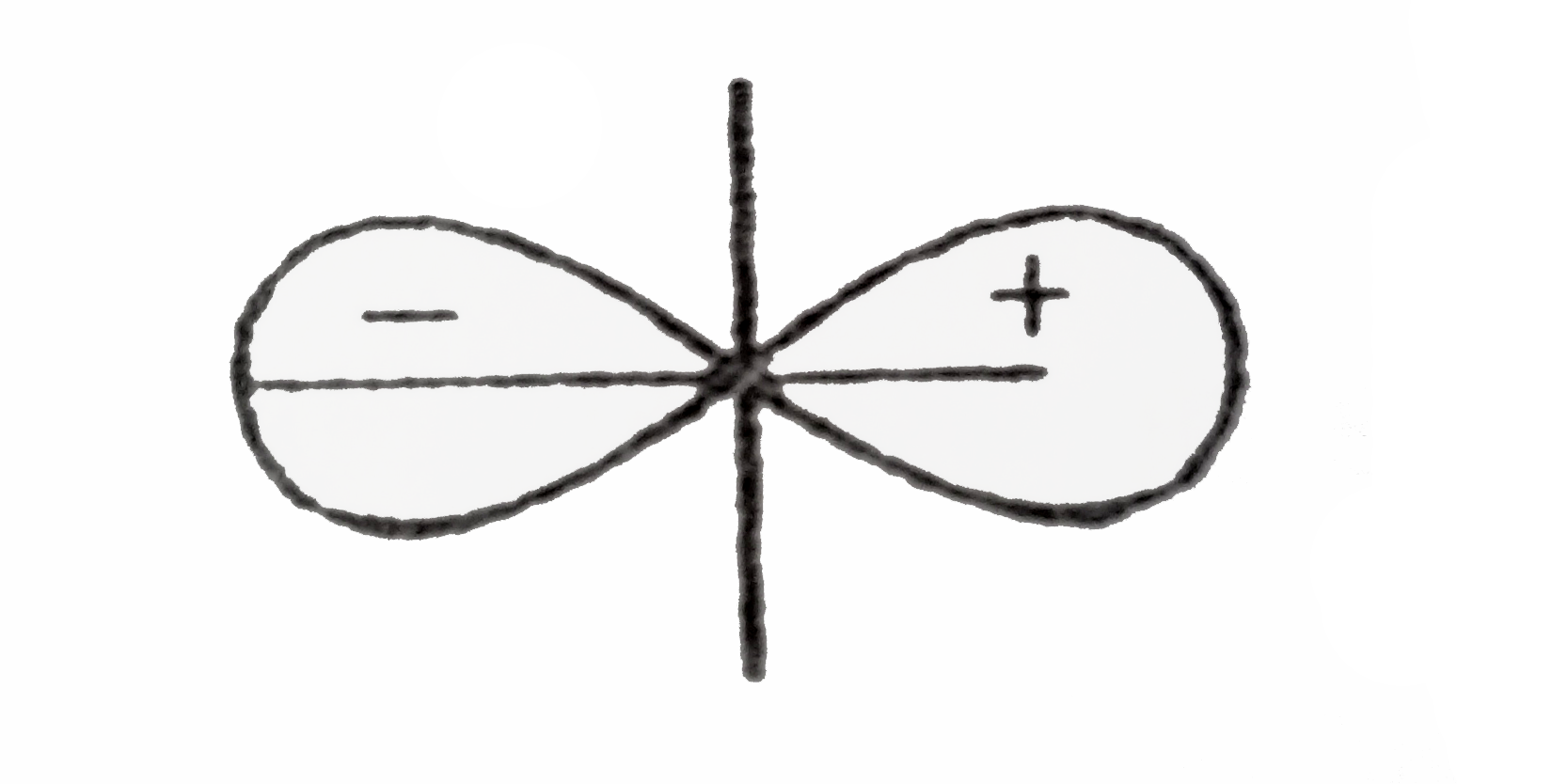
Correct regarding diagram isView SolutionThe Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:
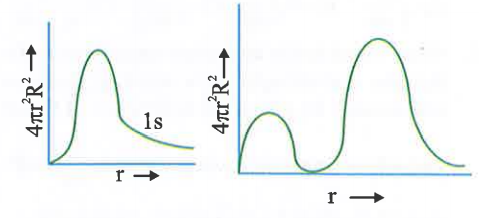
Answer the following questions:
The following graph is plotted for ns-orbitals
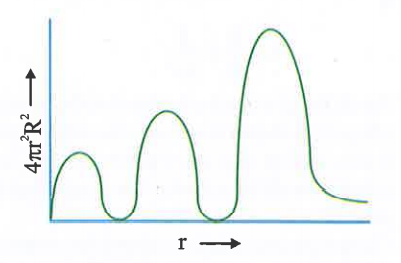
The value of 'n' will be:View Solution

