Two satelites of a planet have period 32 days and 256 days. If the radius of orbit of former is R, find the orbital radius of the latter.
As T2∝R3 or R∝T2/3
∴R2R1=(r2r1)3/2 or R2=R(25632)3/2 = 4R
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE B1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE C1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE A1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions14videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
Similar Questions
Find the mass of the Earth knowing the orbital period and the radius of the Moon.
View SolutionAn artificial satellite of mass m is revolving in a circualr orbit around a planet of mass M and radius R. If the radius of the orbit of satellite be r, then period of satellite is
T=2πR√r3g
Justify the relation using the method of dimensions.View Solution
Knowledge Check
- Question 1 - Select One
The radius of a planet is 74×103km. A satellite of this planet completes one revolution in 16.7 days. If the radius of the orbit of satellite is 27 times the radius of planet, then the mass of planet is
A2.3×1027kgB2.3×1030kgC2.3×1032kgD2.3×1042kg - Question 2 - Select One
If the radius of first Bohr's orbit is r, then radius of second orbit will be
A2rBr2C4rD√2r - Question 3 - Select One
If r is the radius of first orbit, the radius of nth orbit of the H atom will be:
Arn2BrnCrnDr2n2
If a satellite is revolving around a planet of mass M in an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance r from the planet will be given by v2=GM[2r−1a]
View SolutionTwo planets revolve with same angular velocity about a star. The radius of orbit of outer planet is twice the radius of orbit of the inner planet. If T is time period of the revolution of outer planet, find the time in which inner planet will fall into the star. If it was suddenly stopped.
View SolutionThe orbital velocity of a satellite at point B with radius rB and n. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes .12rA find the orbital velocity at (1.2rA):
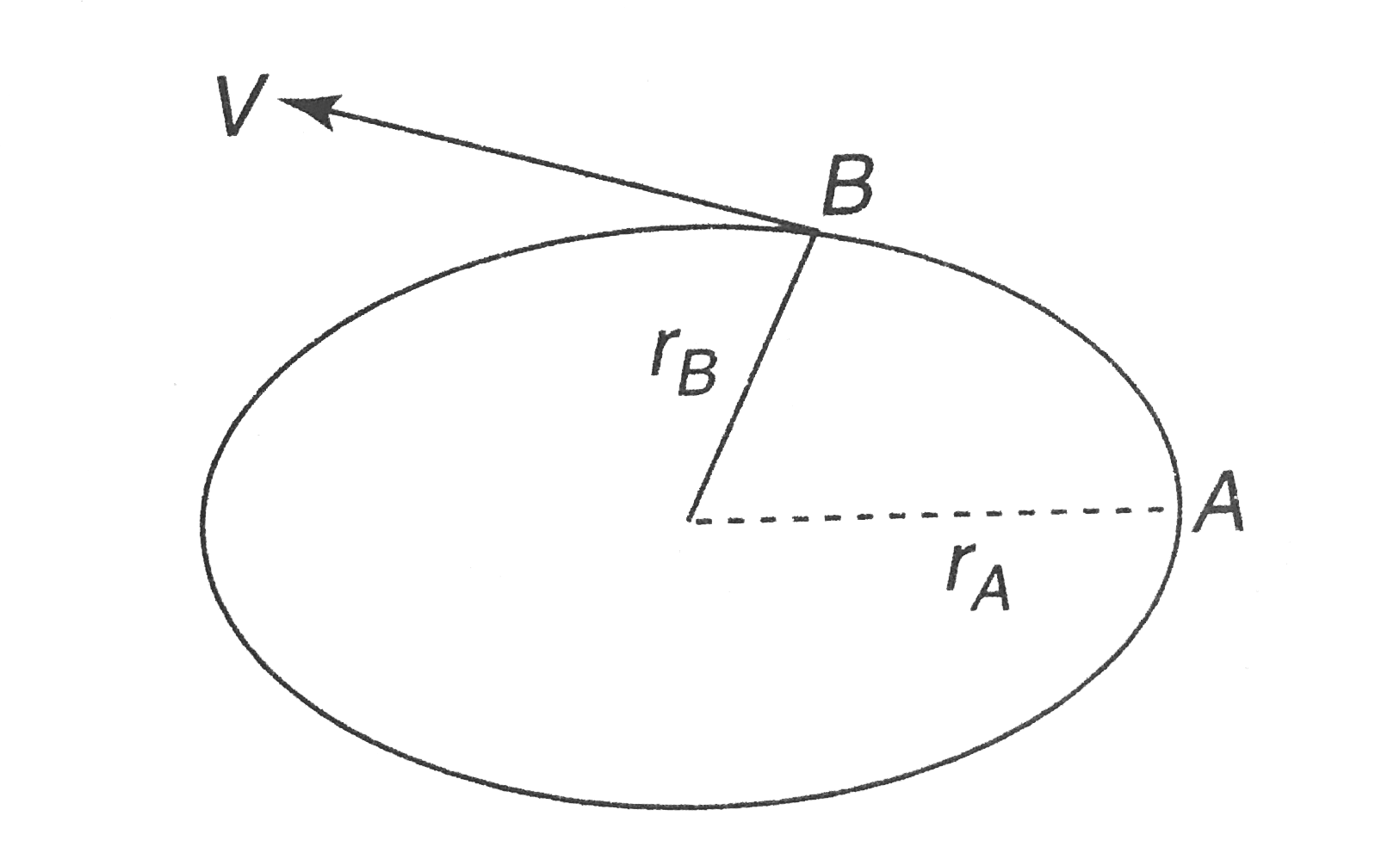 View Solution
View SolutionThe period of a planet around sun is 27 times that of earth the ratio of radius of planet orbit to the radius of earth's orbit is
View SolutionThe work done to increases the radius of orbit of a satellite of mass 'm' revolving around a planet of mass M from orbit of radius R into another orbit of radius 3R is
View Solution

