Three point mass bodies of masses m,2m and 4m are placed at A,B and C as shown in fig. where AB=BC=l.
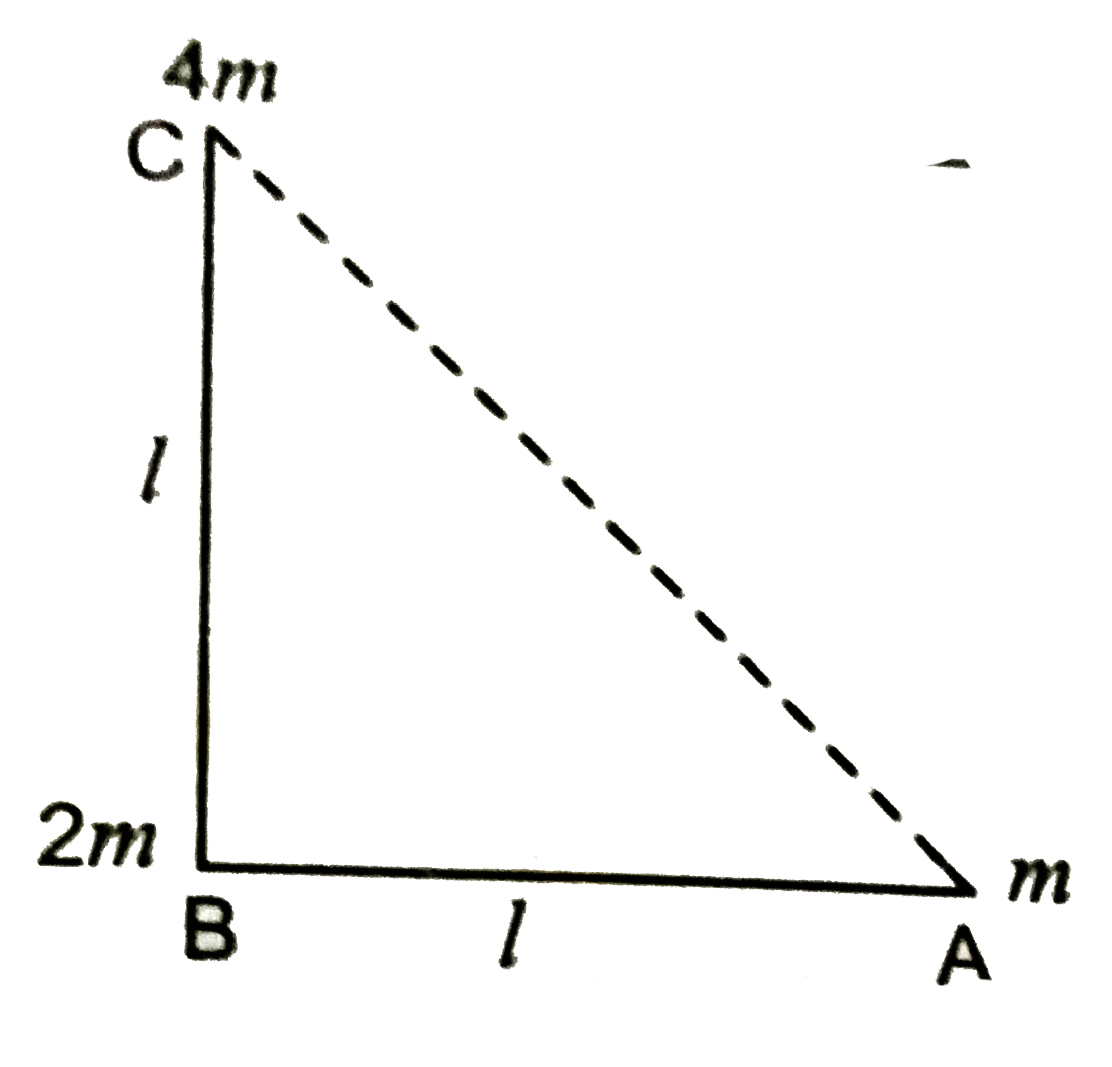
Find the magnitude of the resulatant gravitational pull on body at A due to bodies at B and C.
Refer to Fig. AC=(AB2+BC2)1/2
=(l2+l2)1/2=l√2
Gravitational pull on body at A due to body at B is
F1=Gm×2ml2=2Gm2l2alongAB.
Gravitational pull on body at A due to body at C is
F2=Gm×2m(l√2)2=2Gm2l2alongAC.
As, AB=AC and ∠ABC=90∘ , so ∠BAC=45∘.
i.e., angule θ between −→F1 and −→F2 is 45∘
Using parelogram law of forces, the resultant gravitaitonal force on body at A is
F=√F21+F22+2F1F2cos45∘
=[(2Gm2l2)+(2Gm2l2)2+2×2Gm2l2×2Gm2l2×1√2]1/2
=−2Gm2l2(1+1+√2)1/2=3.696Gm2l2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE B1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE C1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE A1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions14videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
 View Solution
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point due to mass m on the line joining where gravitational field is zero
View Solution
Knowledge Check
- Question 1 - Select One
Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero, is
A−4GMrB−6GmrC−9GmrDzero - Question 2 - Select One
Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
AzeroB−4GmrC−6GmrD−9Gmr - Question 3 - Select One
Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
A−4GmrB−6GmrC−9GmrDzero
Three equal point masses of each mass m are located, respectively at three corners of a square of edge length l as shown in figure. The magnitude of intensity of gravitational field (g) at the fourth corner due to these masses is
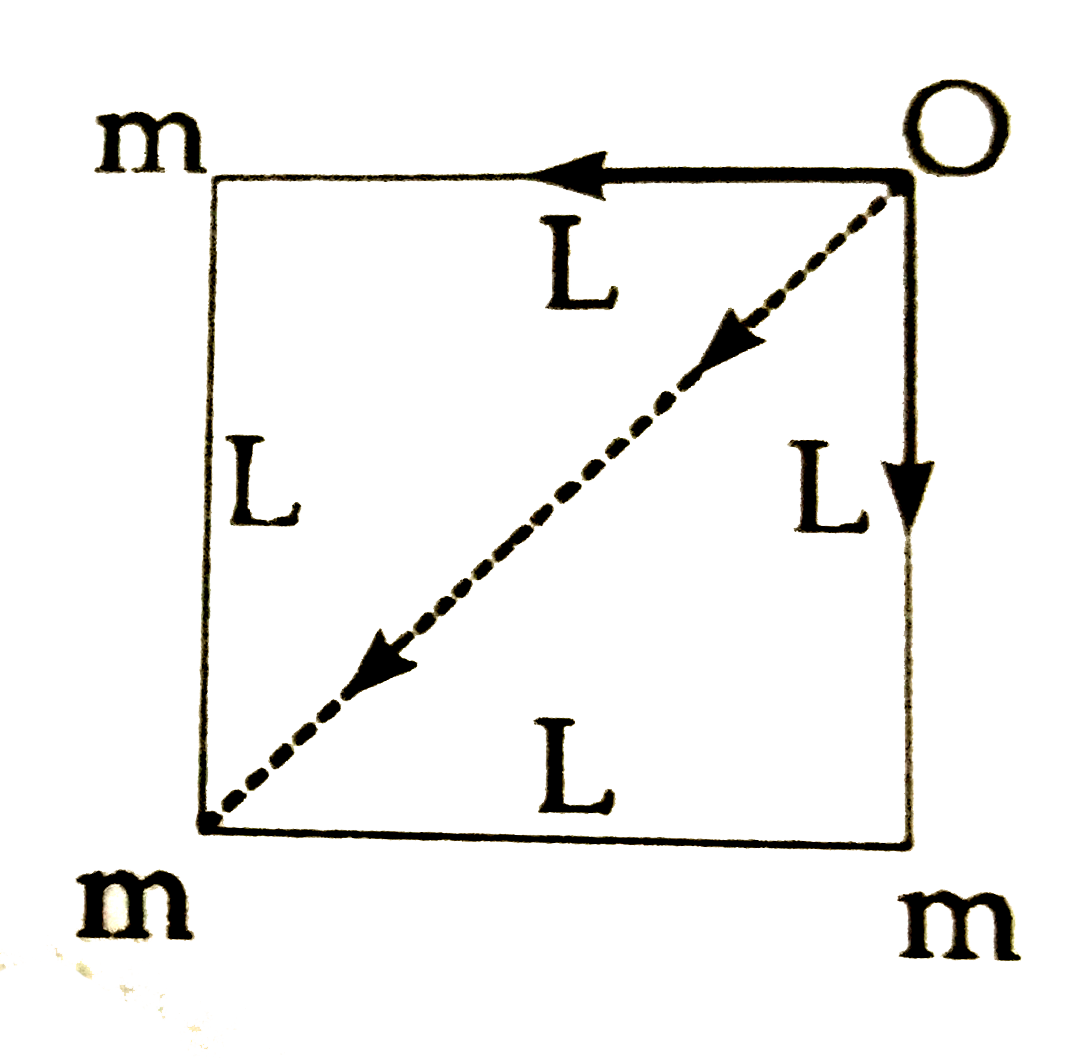 View Solution
View SolutionTwo point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B
 View Solution
View SolutionTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionTwo particle of masses m and 2m are at a distance 3r apart at the ends of a straight line AB. C is the centre of mass of the system. The magnitude of the gravitational force on a unit mass placed at C due to the masses is
View SolutionEqual forces F act on isolated bodies A and B as shown in figure. The mass of B is three times that of A. The magnitude of the acceleration of A is:
View Solution

