A wire of length l and radius r has a weight W and the Young's modulus of elasticity Y. it is suspended vertically from a fixed point. Calculate the increase in length of wire porduced due to its own weight.
Since the tension is non- uniform along the wire, we have variable stress in wire. Let us consider a small element of length dx at a distance x from bottom end P. fig.
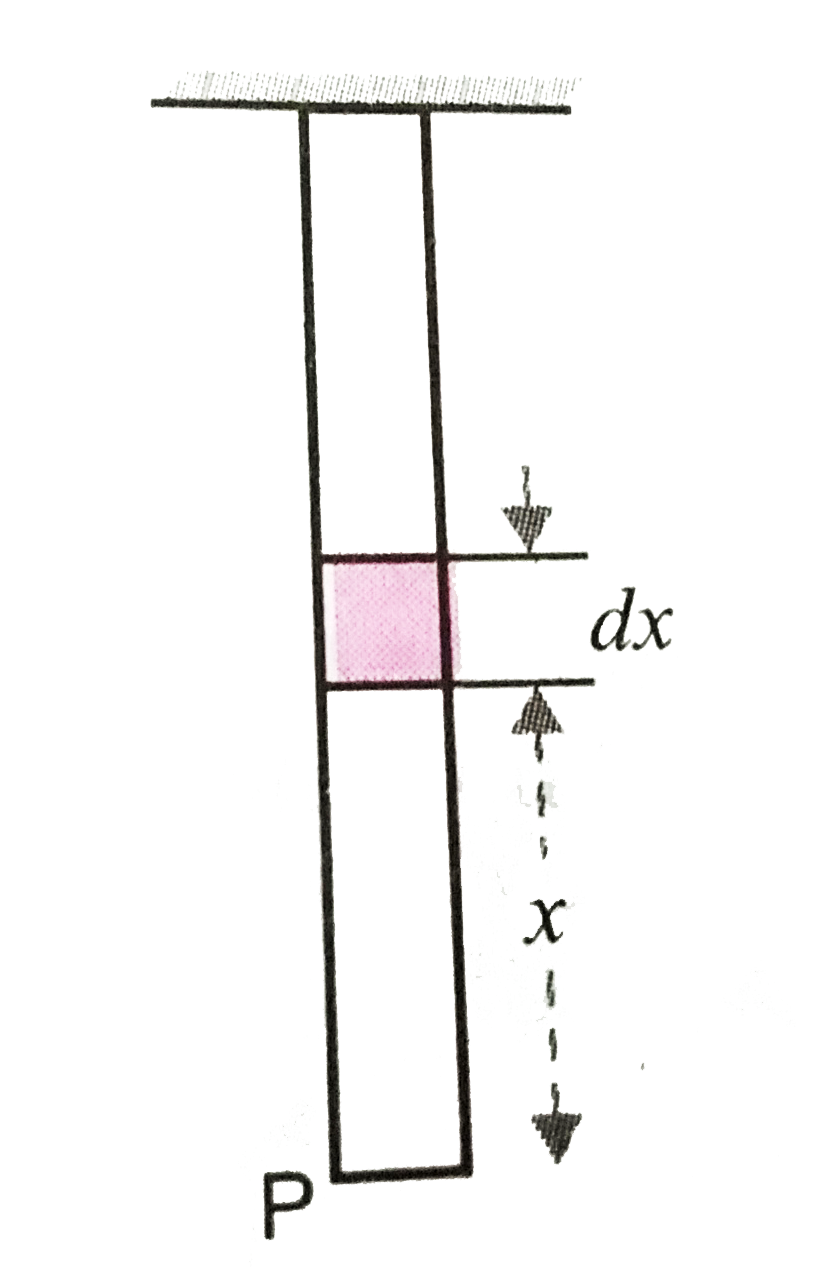
The tension in the element of the wire
=mglx
If dl is the increase in length of the element,
then longitudinal strain = dldx
Normal stress =mgxl×1πr2
∴Y=mgxlπr2/dldxordl=mgxdxYπr2l
Total change in length of wire is
Δl=∫l0mgxdxYπr2l=mgYπr2l×l22=mgl2Yπr2.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions73videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Solved Examples159videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
wire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View SolutionA bar of mass m and length l is hanging from point A as shown in the figure . If the Young's modulus of elasticity of the bar is Y and area of cross - section of the wire is A, then the increase in its length due to its own weight will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thick rope of density ρ and length L is hung from a rigid support. The increase in length of the rope due to its own weight is (Y is the Young's modulus)
A0.14YρL2gB12YρL2gCρL2gYDρLgY - Question 2 - Select One
An iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
A0.2 mmB0.5 mmC2 mmD1 mm - Question 3 - Select One
A rubber cord of density d, Young's modulus Y and length L is suspended vertically . If the cord extends by a length 0.5 L under its own weight , then L is
AY2dgBYdgC2YdyDdg2Y
A uniform wire of length L and radius r is twiste by an angle aplha. If modulus of rigidity of the wire is, then the elastic potential energy stored in wire
View SolutionA uniform wire of length 1 and radius r has resistance 100Ω. it is recast into a thin wire of (i) length 2l (ii) radius r/2. Calculate the resistance of new wire in each case.
View SolutionA uniform wire of length l and radius r has a resistance of 100Ω. It is recast into wire of radius R2
View SolutionIf Y is the Young's modulus of a wire of cross sectional area A, then the force required to increase its length by 0.1% will be
View SolutionIncrease in length of a wire is 1 mm when suspended by a weight. If the same weight is suspended on a wire of double its length and double its radius, the increase in length will be
View Solution
