Question

A steel rod of length 2l cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through its centre and perpendicular to its length with constant angular velocity $\omega$. If Y is the Young's modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)

Explanation

Refer

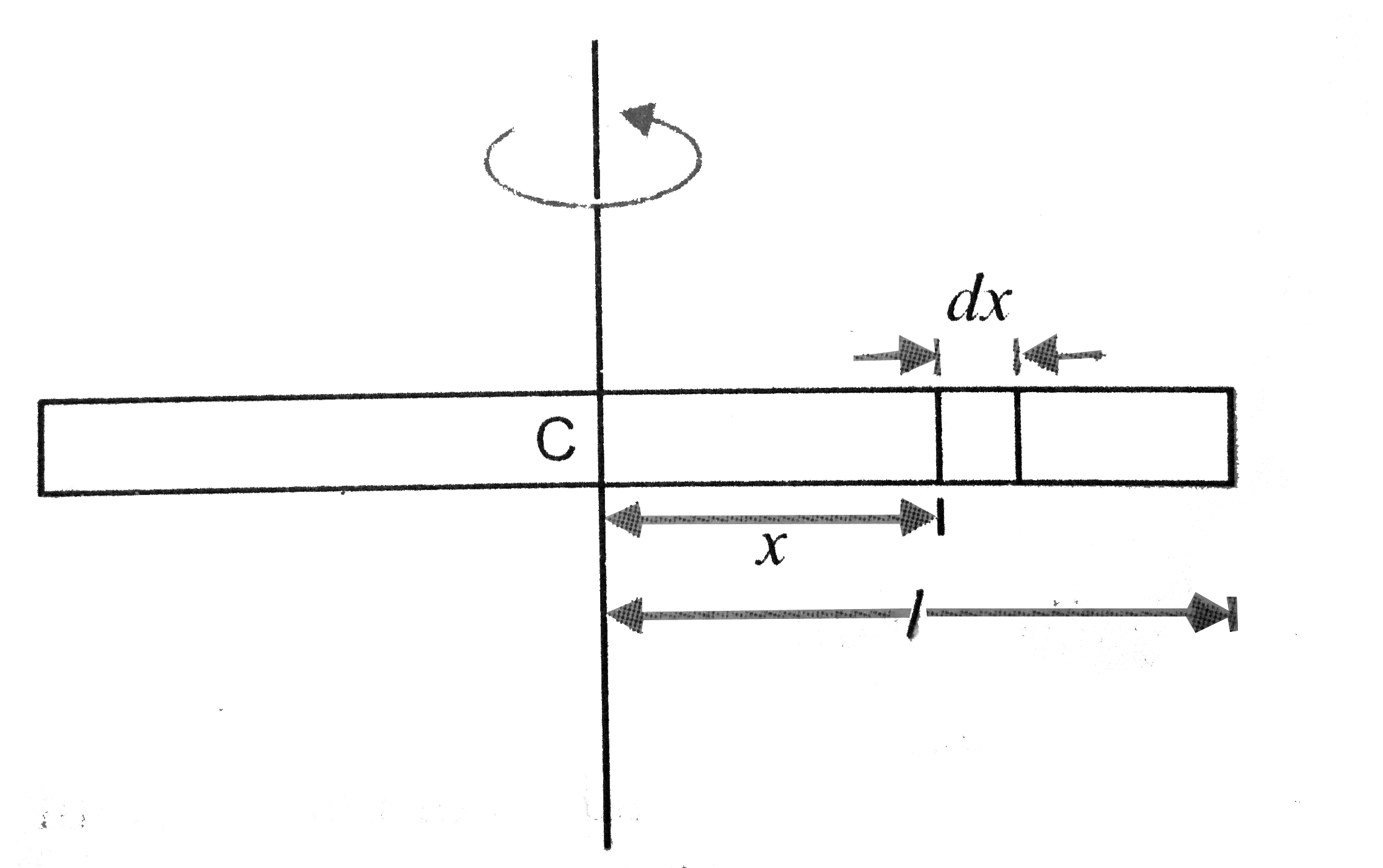
Mass per unit length of rod = M//2l. Consider a small element of length dx at a distance x from the centre C of the rod. Mass of the element, `dm = (M)/(2l)dx` Centripetal force acting on the samll element is `dF = (dm)xx omega^2 = ((M)/(2l)dx) x omega^2 = (M omega^2)/(2l) x dx` As this force is provided by tension in the rod due to eleasticity, so the tension T in the rod at a distnace x from the axis of roataion will be the centripetal force due to all elements in the rod between x = x to x = l. There, `T = int_x^l (M omega^2)/(2l) xdx = (M omega^2)/(2l) ((l^2)/(2) - (x^2)/(2)) = (M omega^2)/(4l) (l^2 -x^2)`
Let dy be the increases in length of the element of lenght dx, then `Y = (T dx)/(A dy) or dy = (T dx)/(YA) = (M omega^2 (l^2 - x^2))/(4l xx YA) dx`
Total extension in the rod is `Y = int_(-l) ^(+l) (Momega^2)/(4l YA) (l^2 - x^2) dx= (2 M omega^2)/(4l YA) int_0^l (l^2 - x^2)dx`
`=(M omega^2)/(2 lYA) [ l^3 -(l^3)/(3)] = M omega^2 xx (2l^3)/(3) = (M omega^2 l^2)/(3YA)`