A uniform rod of mass m and length l is rotating with constant angular velocity $ω$ about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:

$\frac{m n^{2} l}{8 A y}$

$\frac{3 m ω^{2} l}{8 A y}$

$\frac{3 m ω^{2} l}{4 A y}$

$\frac{m ω}{4 A y}$

Video Solution

Text Solution

Verified by Experts

$d T = d m (l - x) ω^{2}$
$d T = \frac{m}{l} d x (l - x) ω^{2}$
$\Rightarrow \int_{0}^{T} d T = \int_{0}^{l / 2} \frac{m ω^{2}}{l} (l 0 x) d x$

$\frac{m ω^{2}}{l} {[l x - \frac{x^{2}}{2}]}_{0}^{l / 2} = \frac{m ω^{2}}{l} [\frac{l^{2}}{2} - \frac{l^{2}}{g}]$
$∴$ Tension at mid point is:
$T = \frac{3}{8} m l ω^{2} \Rightarrow$ stress $= \frac{3 m l ω^{2}}{8 A}$
$\Rightarrow$ strain $\frac{3 m l ω^{2}}{8 A Y}$
Alternatively Tension at mid point can be found by using

$F_{ext} = m a_{c m}$
$T = \frac{m}{2} (ω^{2} \frac{3 l}{4}) = \frac{3}{8} m ω^{2} l$

Updated on:21/07/2023

A uniform rod of length l is rotating in a gravity free region about an axis passing through its one end and perpendicular to it length. Choose graph between stress developed and distance the axis of roation.
A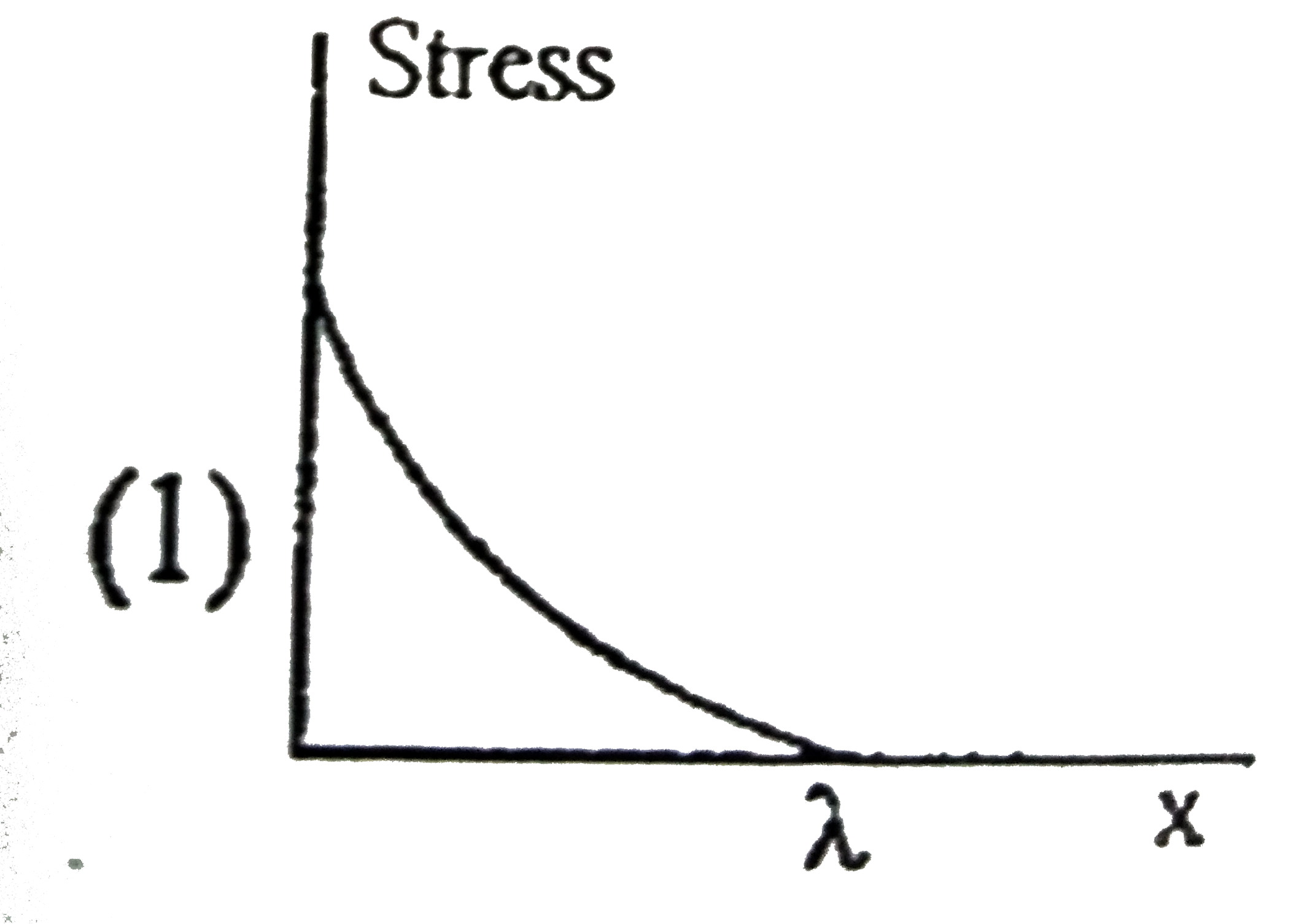
B
C
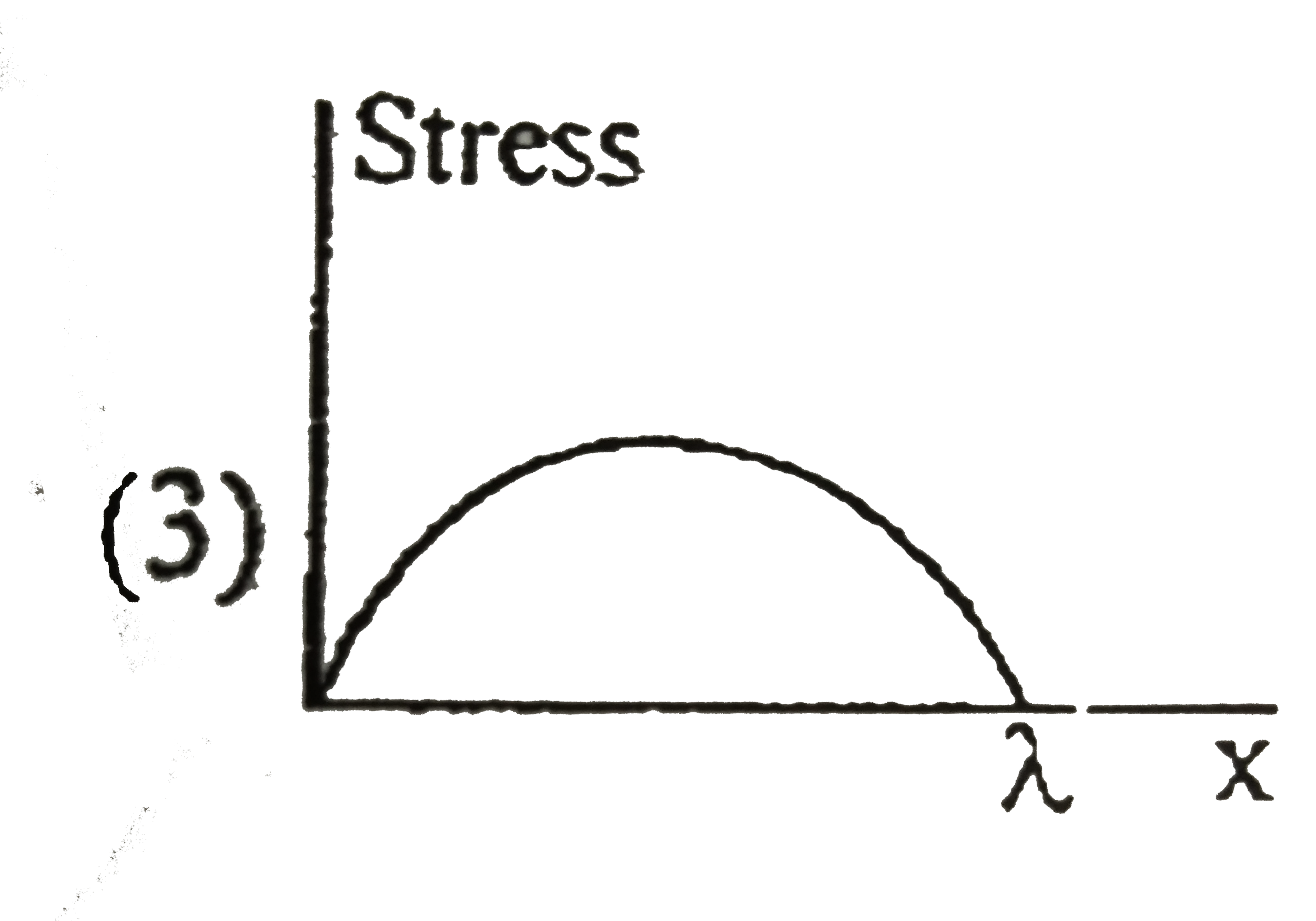D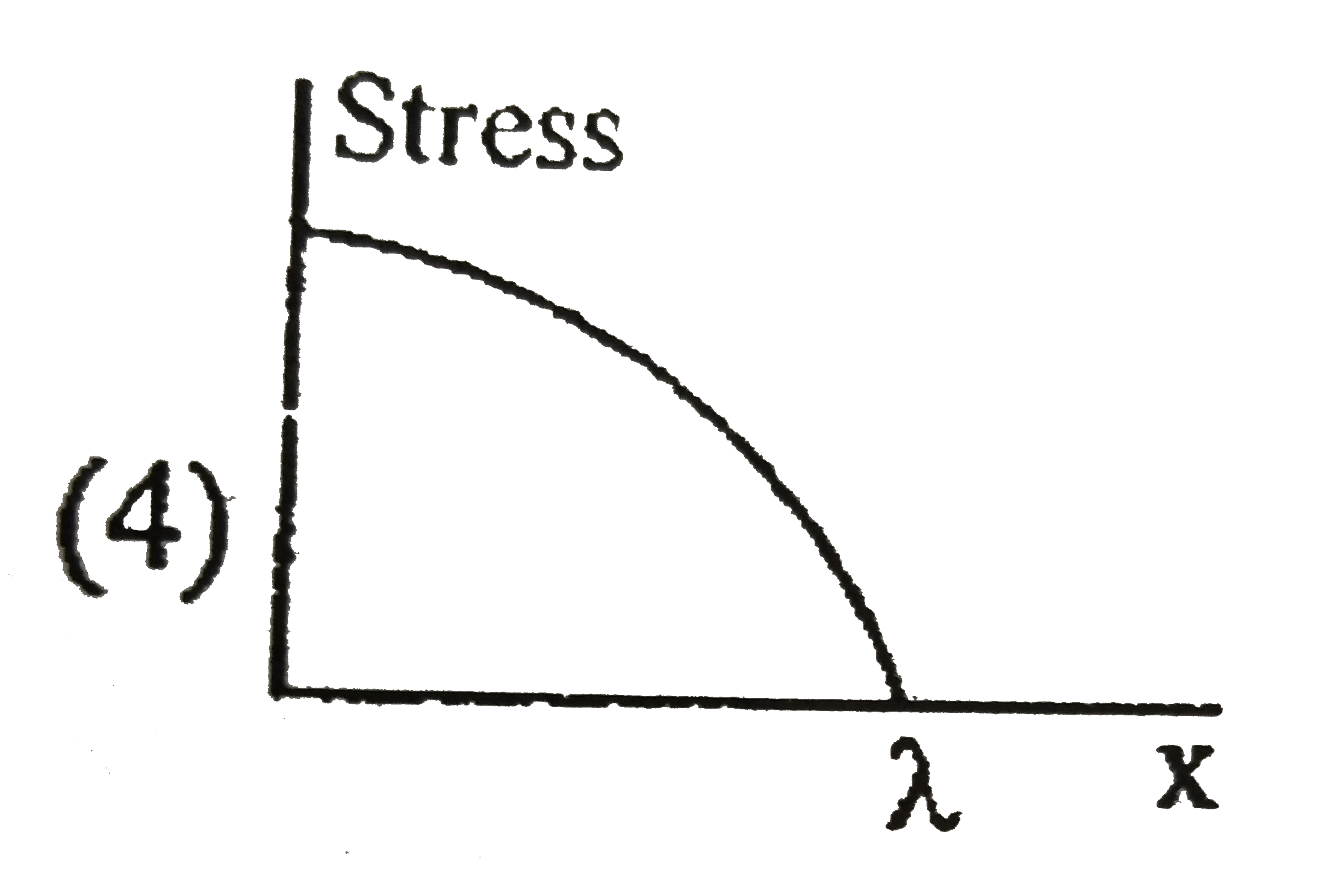
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
The radius of gyration of a uniform rod of length $l$ about an axis passing through one of its ends and perpendicular to its length is
A $\frac{l}{\sqrt{2}}$
B $\frac{l}{3}$
C $\frac{l}{\sqrt{3}}$
D $\frac{l}{2}$