A liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
(a) As the top face B of cylinder is in contact with atmospherice air, so the pressure at B is atmospheric pressure i.e. PB=P0 (b) The pressure at C is due to atmospherice air and also de to weight of the cylinder, i.e., PC=P0+MgA (c ) The pressure at D is due to atmospheric air, weight of cylinder and weight of liquid in cylinder i.e., PD=P0+(Mg+HρgA)A=P0+MgA+Hρg (d) in the absence of gravity i.e., the system is in free fall (as is in satellite), then g =0 in this case PB=PC=PD=P0.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question
5 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Test Your Grip A
10 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions
73 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A liquid of density ρ is filled in a beaker of cross section S to a height H and then a cylinder of mass m and corss section s is made to float in it as shown in figure. It the atmospheric pressure is p0, find the pressure a at the top face A of the cylinder b at the botom face C of the cylinder and c. at the base B of the beaker. Can ever these three pressures be equal?

View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDgA solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
AπklA2B2πklA2CπklADNoneIn the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
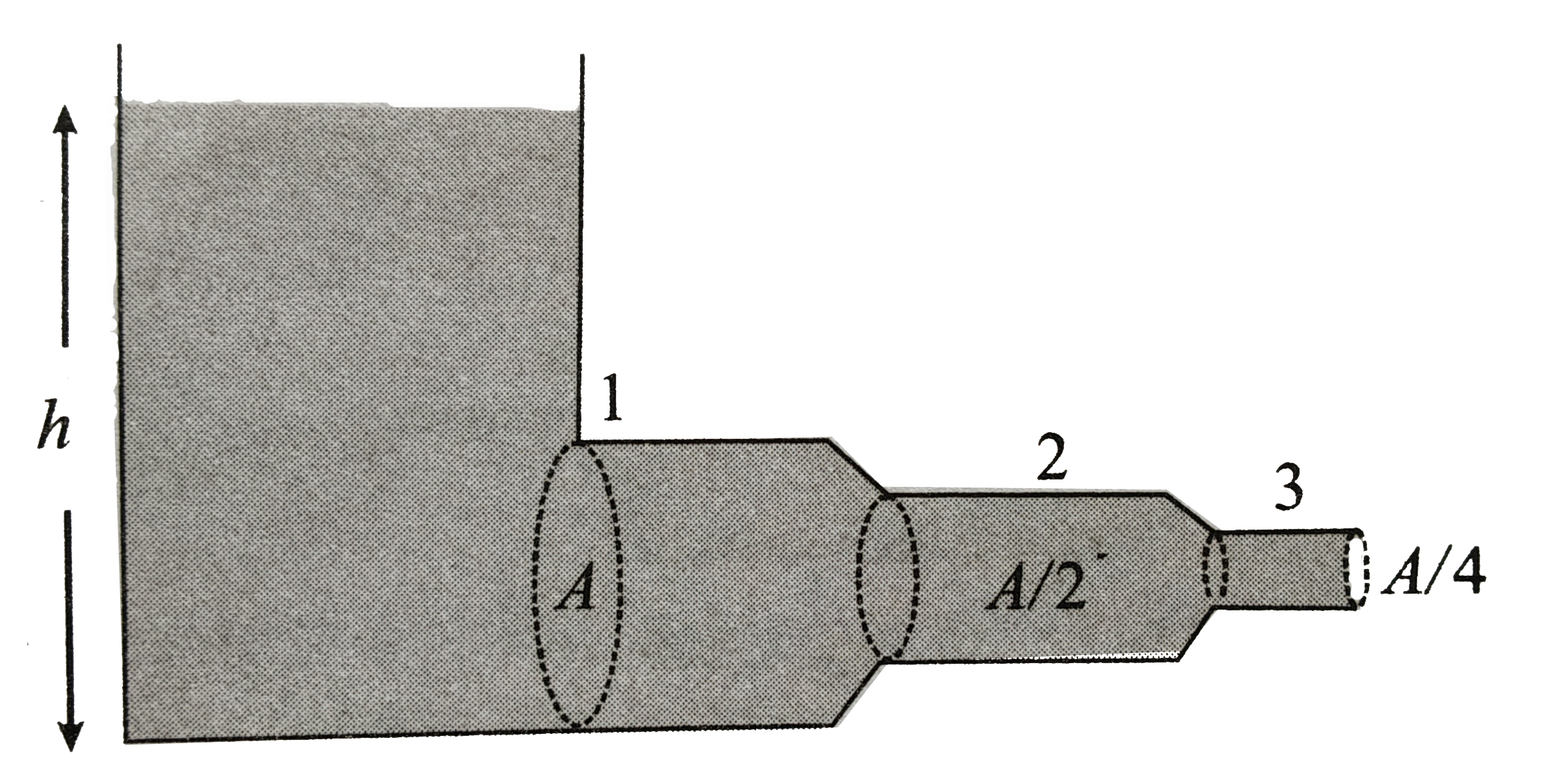 A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4
A√2hg,P0+ρhg2B√hg,P0+ρhg2C√hg2P0+3ρhg4D√hg2,P0+3ρhg4
A cylinder contains He at 2 atmosphere pressure and hydrogen at 1.5 atmosphere pressure. What is the pressure of the mixture of gases in the cylinder ?
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
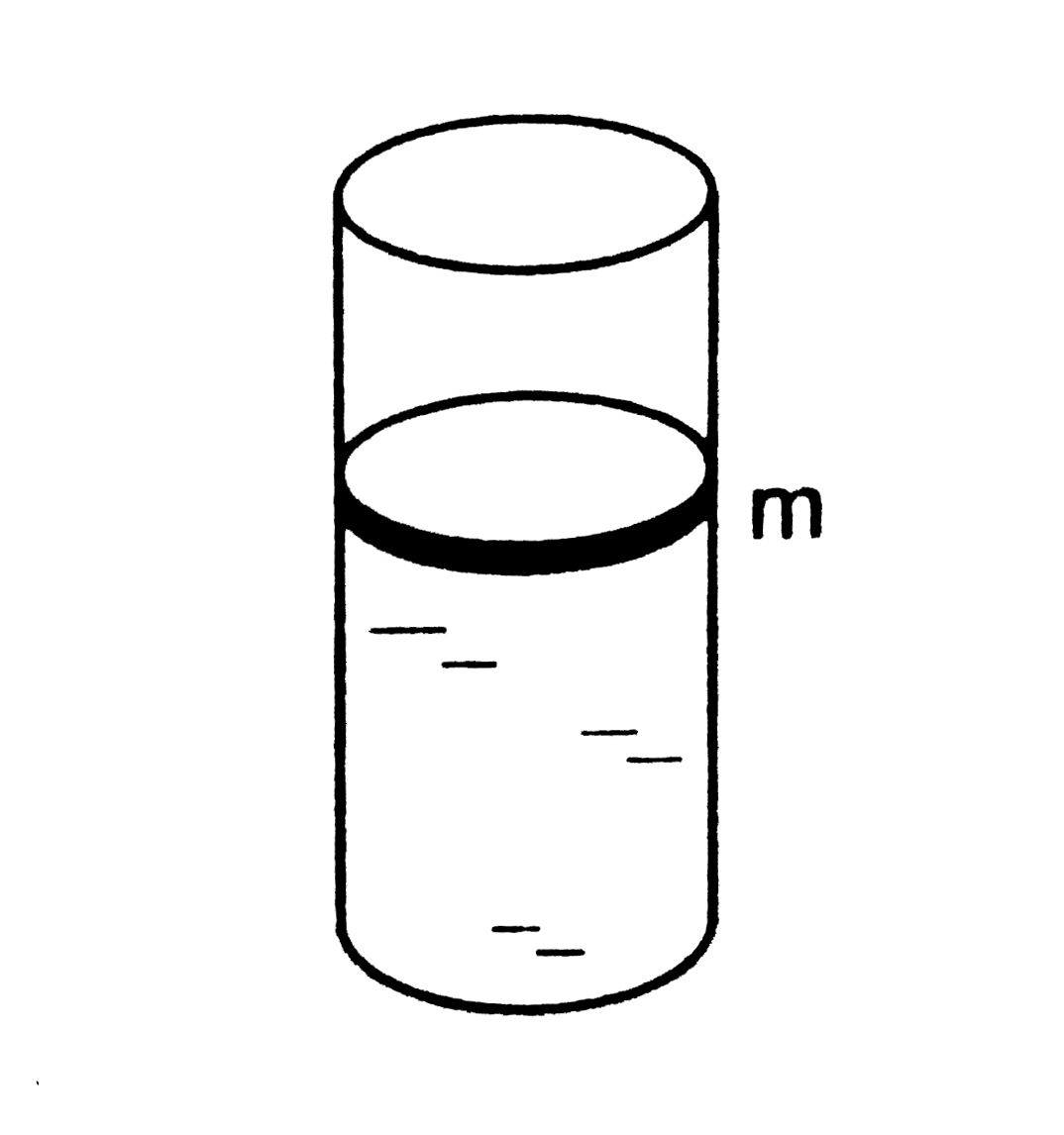 ,
,
View SolutionIf a solid cylinder of area of cross-section A is moving with velocity V in medium of density p then power loss of cylinder is
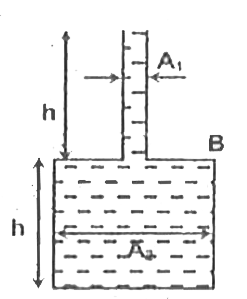
View SolutionThe vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
View SolutionA cylinder of certain mass is held in vertical position. If the height of the cylinder is 10 cm and radius of cross - section is 4 cm such that the pressure acting on its bottom surface is 21560N m−2 , find the mass of the cylinder ?
View Solution
