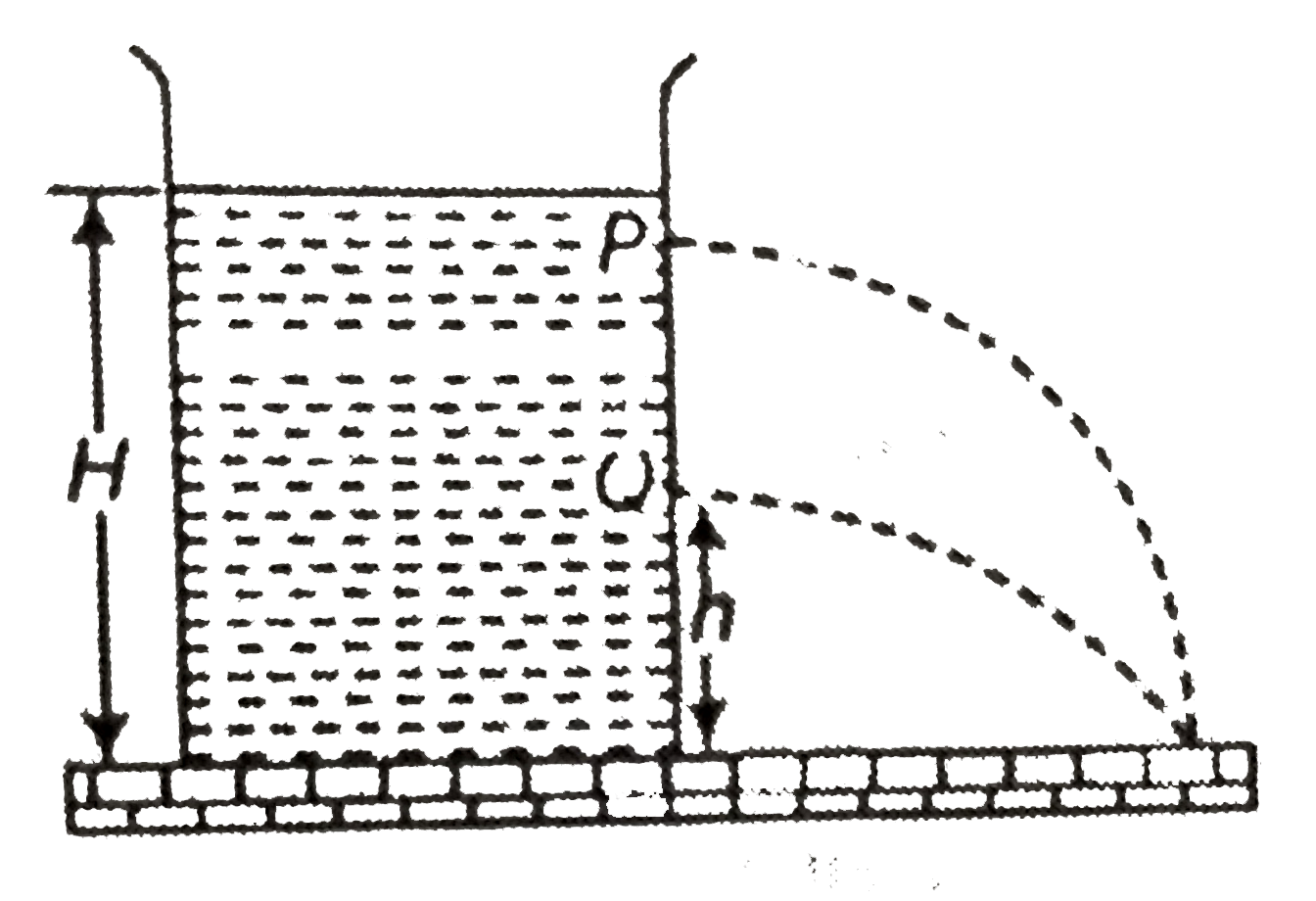
A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
The correct Answer is:B
To solve the problem of finding the depth h from the free surface of water for maximum range when water flows out of a hole in a cylindrical vessel, we can follow these steps:
1. Identify the parameters:
- Let H be the height of the water in the cylindrical vessel.
- Let h be the depth of the hole from the free surface of the water.
2. Determine the velocity of water exiting the hole:
- The velocity U of water exiting the hole can be calculated using Torricelli's theorem:
U=√2gh
- Here, g is the acceleration due to gravity.
3. Calculate the time of flight:
- The water will fall a vertical distance of H−h before it reaches the ground. Using the equation of motion:
Sy=Uyt+12gt2
- Since the initial vertical velocity Uy=0:
H−h=12gt2
- Rearranging gives:
t2=2(H−h)g
- Thus, the time t is:
t=√2(H−h)g
4. Calculate the horizontal range:
- The horizontal range R can be calculated as:
R=U⋅t
- Substituting for U and t:
R=√2gh⋅√2(H−h)g=2√h(H−h)
5. Maximize the range:
- To find the maximum range, we need to differentiate R with respect to h and set the derivative to zero:
R=2√h(H−h)
- Let R2=4h(H−h). Differentiate R2:
d(R2)dh=4(H−2h)=0
- Setting the derivative to zero gives:
H−2h=0⟹h=H2
6. Conclusion:
- For maximum range, the depth h from the free surface of water should be:
h=H2
Final Answer:
The value of h for maximum range is H2.
- Let H be the height of the water in the cylindrical vessel.
- Let h be the depth of the hole from the free surface of the water.
- The velocity U of water exiting the hole can be calculated using Torricelli's theorem:
U=√2gh
- Here, g is the acceleration due to gravity.
- The water will fall a vertical distance of H−h before it reaches the ground. Using the equation of motion:
Sy=Uyt+12gt2
- Since the initial vertical velocity Uy=0:
H−h=12gt2
- Rearranging gives:
t2=2(H−h)g
- Thus, the time t is:
t=√2(H−h)g
- The horizontal range R can be calculated as:
R=U⋅t
- Substituting for U and t:
R=√2gh⋅√2(H−h)g=2√h(H−h)
- To find the maximum range, we need to differentiate R with respect to h and set the derivative to zero:
R=2√h(H−h)
- Let R2=4h(H−h). Differentiate R2:
d(R2)dh=4(H−2h)=0
- Setting the derivative to zero gives:
H−2h=0⟹h=H2
- For maximum range, the depth h from the free surface of water should be:
h=H2
The value of h for maximum range is H2.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Integer Type Questions
Explore 12 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Asseration - Reason Type Question
Explore 18 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-II
Explore 14 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A tank is filled with water to a height H. A hole is punched in the wall at a depth h below the water surface. Find the distance x from the wall at which the stream strikes the floor. Could a hole be punched at another depth so that this second stream would have the same range? If so at what depth? For what value of h is range maximum?
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
View Solution
Knowledge Check
A cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
 Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrongA tank with vertical walls is mounted so that its base is at a height H above the horizontal ground. The tak is filled with water to a depth h. A hole is puched in the side wall of the tank at a depth x below the water surface. To have maximum range of the emerging stream, the value of x is
AH+h4BH+h2CH+h3D3(H+h)4A tank with vertical walls is monted so that its base is at height of 1.2 m above the horizotnal ground. The tank is filled with water to depth 2.8 m. A holw is punched in the side wall of the tank at a depth x m below the surface of water to have maximum range of the emerging stream. then the value of x in metre is
A4B1.6C2D2.3
A tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D
 .
.
View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View Solution
