A spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r(rltR), then the correct option(s) is (are)
P(r=0)=0
P(r=3R/4)P(r=2R/3)=6380
P(r=3R/5)P(r=2R/5)=1621
P(r=R/2)P(r=R/3)=2027
The correct Answer is:B, C
Consider a spherical element of linner radius r and outer radius (r + dr) as shown in
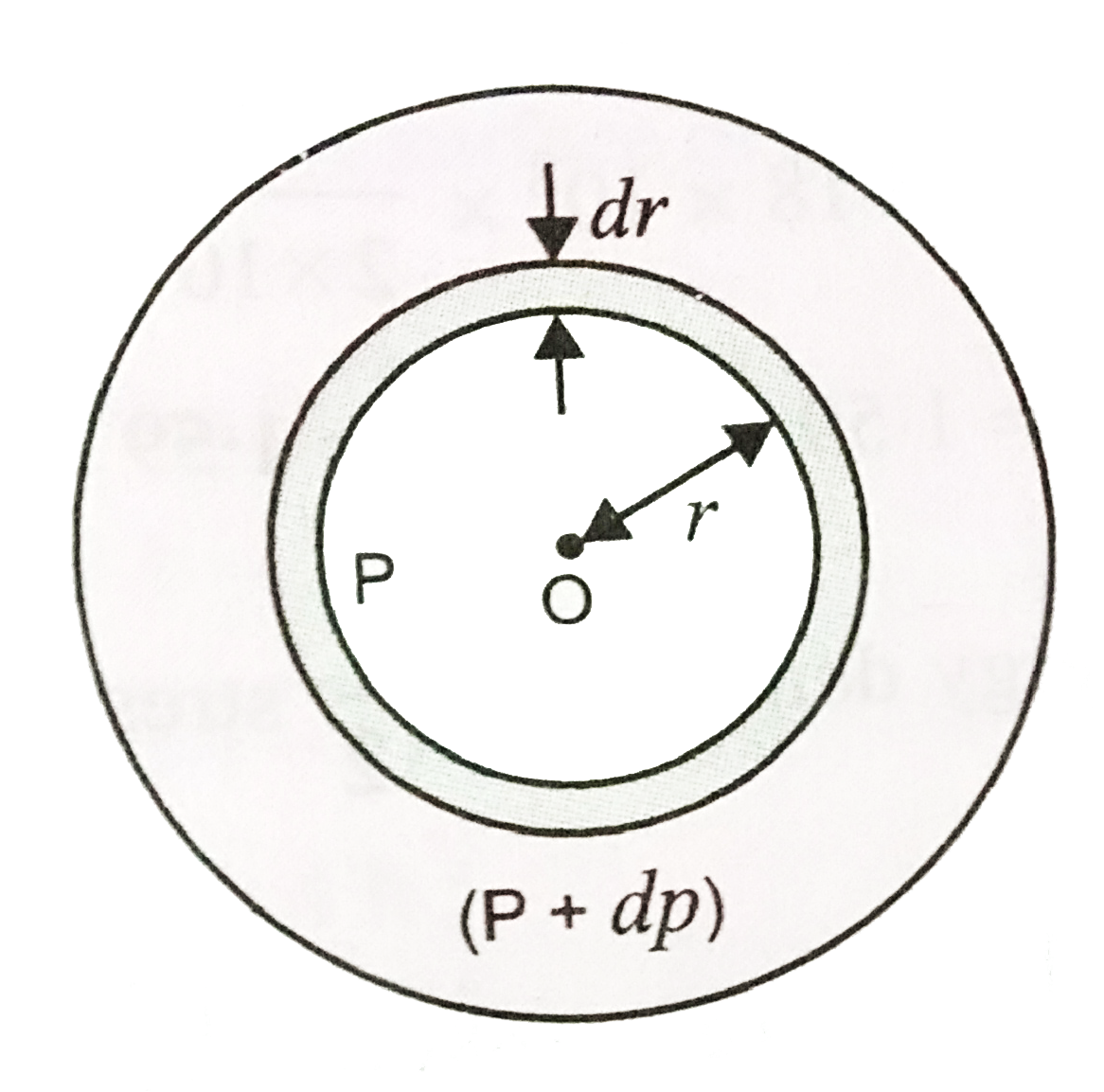
Let g be the ac celeration due to gravity at the location of the element which is at distance r from the center O. In equilibrium, the difference in pressure (dp) on the two sides of the element is pressure by gravity per unit area.
So −dp=ρgdr
If m is the mass of spherical body of radius r, then
m=43πr2ρ and g=Gmr2=Gr2×43πr3ρ=43πGρr
∴dp=−ρ(43πGρr)dr=−43πρ2Grdr
∫P(=r)P(=R)dp=−43πGρ2∫r=rr=Rrdr
or P(r)−P(R)=43πGρ2(R2−r22)
Put P(R)=0 , then P(r)=43πGρ2(R2−r2)2
(a) When r=0,P(r)=43πGρ2R22.
Thus, option (a) is wrong.
(b) P(r=3R/4)P(r=2R/3)=R2−(3R/4)2R2−(2R/3)2=7/165/9=6380.
Thus, option (b) is true.
(c) P(r=3R/5)P(r=2R/5)=R2−(3R/5)2R2−(2R/5)2=16/2521/25=1621
Thus, option (c) is true.
(d) P(r=R/2)P(r=R/3)=R2−(R/2)2R2−(R/3)2=3/48/9=2732.
Thus, option (d) is wrong.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA star can be considered as a shpherical ball of hot gas of radius R.Inside the star the density of the gas is ρr at a radius r and mass of the gas within this region is Mr.The correct differential equation for variation of mass with respect to radius (dMrdt) is (refer to the adjacent figure)

A star in its prime age is said to be under equilibrium due to gravitational pull and outward radiation pressure (ρ).Consider the shell of thickness dr . If the pressure on this shell is dp then the correct equation is (G is universal gravitational constant)
View Solution
Knowledge Check
A spherical black body of radius n radiates power p and its rate of cooling is R. then.
Ap∝nBp∝n2CR∝n2DR∝1nA spherical marble of radius r is made to oscillate in a bowl of radius R. What is its period of oscillation ?
AT=2π√RgBT=2π√R−rgCT=12π√gR−rDT=2π√gRA spherical solid blakc body of radius 'r' radiates power 'H' and its rate of cooling is 'C'. If density is constant then which of the following is/are true.
AH∝randC∝r2BH∝r2andC∝1rCH∝randC∝r3DH∝r2andC∝r
A small spherical body of radius r is falling under gravity in a viscous medium. Due to friction the meduim gets heated. How does the rate of heating depends on radius of body when it attains terminal velocity?
View SolutionA body is in equilibrium under the action of three coplanar forces P,QandR as shown in figure. Select the correct statement.
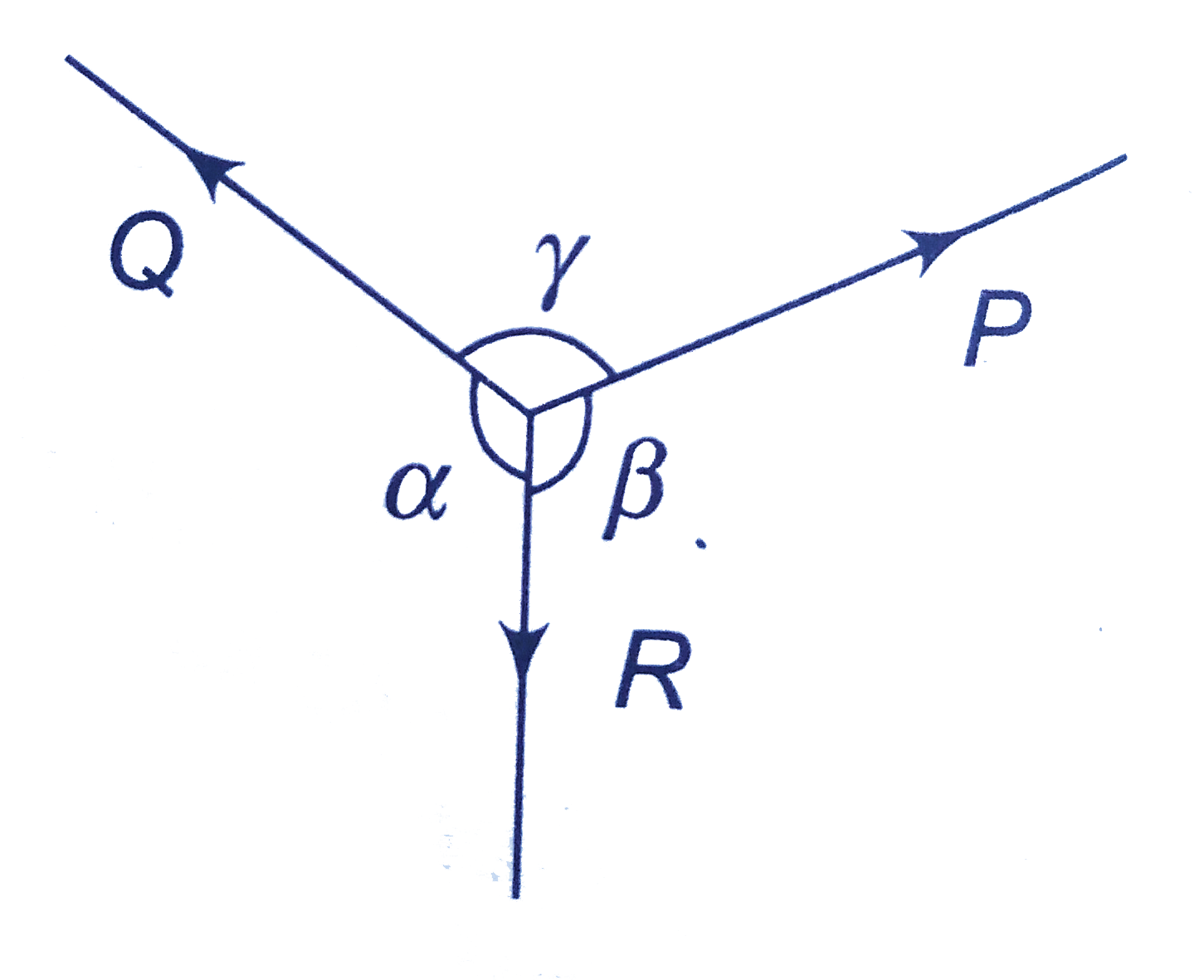
View SolutionA star can be considered as spherical ball of hot gas of radius R. Inside the star, the density of the gas is ρr at radius r and mass of the gas within this region is Mr.
A star in it's prime age is said to be under quilibrium due to gravitational pull and outward radiation pressure (p). consider the shell of thikness dr as in the figure of previous question. if the pressure on this shell is dp then the correc equation is (G is universal gravitational constant)
View SolutionA star can be considered as spherical ball of hot gas of radius R. Inside the star, the density of the gas is ρr at radius r and mass of the gas within this region is Mr.
The correct differential equation for variation of mass with respect to radius is (refer to the adjacent figure)
View SolutionAssuming the Sun to be a spherical body of radius R at a temperature of TK, evalute the total radiant powerd incident of Earth at a distance r from the sun
where r0 is the radius of the Earth and σ is Stefan's constant.
View Solution
