A spring compressed by 0.1m develips a restoring force 10N. A body of mass 4kg is placed on it. Deduce (i) the force constant of the spring (ii) the depression of the spring under the weight of the body ( take g=10N/kg) and (iii) the period of oscillation, if the body is left free.
Let's solve the question step by step.
Given:
- Compression of the spring, ΔL=0.1m
- Restoring force, F=10N
- Mass of the body, m=4kg
- Acceleration due to gravity, g=10N/kg
(i) Finding the force constant of the spring k:
The force constant k of a spring is defined by Hooke's Law, which states that the restoring force F is proportional to the displacement ΔL:
F=kΔL
Rearranging the formula to find k:
k=FΔL
Substituting the known values:
k=10N0.1m=100N/m
(ii) Finding the depression of the spring under the weight of the body y:
When the body is placed on the spring, the weight of the body exerts a force on the spring, which can be calculated as:
Weight=m⋅g=4kg⋅10N/kg=40N
Using Hooke's Law again, we can find the depression y caused by this weight:
F=ky
Rearranging for y:
y=Fk
Substituting the values:
y=40N100N/m=0.4m
(iii) Finding the period of oscillation T:
The period of oscillation for a mass-spring system is given by the formula:
T=2π√mk
Substituting the known values:
T=2π√4kg100N/m
Calculating the square root:
T=2π√0.04=2π⋅0.2=0.4π
Calculating 0.4π:
T≈1.256s(approximately 1.26s)
Summary of Results:
1. Force constant of the spring k=100N/m
2. Depression of the spring under the weight of the body y=0.4m
3. Period of oscillation T≈1.26s
---
- Compression of the spring, ΔL=0.1m
- Restoring force, F=10N
- Mass of the body, m=4kg
- Acceleration due to gravity, g=10N/kg
1. Force constant of the spring k=100N/m
2. Depression of the spring under the weight of the body y=0.4m
3. Period of oscillation T≈1.26s
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION2videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - SOLVED EXAMPLES54videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
A spring compressed by 0.2 m develops a restoring force of 25 N. A body of mass 5 kg is placed over it. Deduce (i) force constant of the spring (ii) the depression of the spring under the weight of the body and (iii) the period of oscillation, if the body is disturbed. Take g=10Nkg−1.
View SolutionOn compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.View Solution
Knowledge Check
- Question 1 - Select One
When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/m - Question 2 - Select One
If a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
A1.22 rad/sB2.22 rad/sC3.22 rad/sD4.22 rad/s - Question 3 - Select One
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)
 A2π√M2KB2π√2MKC2π√MSinθKD2π√2MSinθK
A2π√M2KB2π√2MKC2π√MSinθKD2π√2MSinθK
A spring is compressed by 10 cm by a ball of mass 20 g . What will be the potential energy of a spring if the force constant of the spring is 20 N cm−1 .
View SolutionFigure shows a force compression curve of a spring. A body of mass 5kg moving with the velocity of 8m/s hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
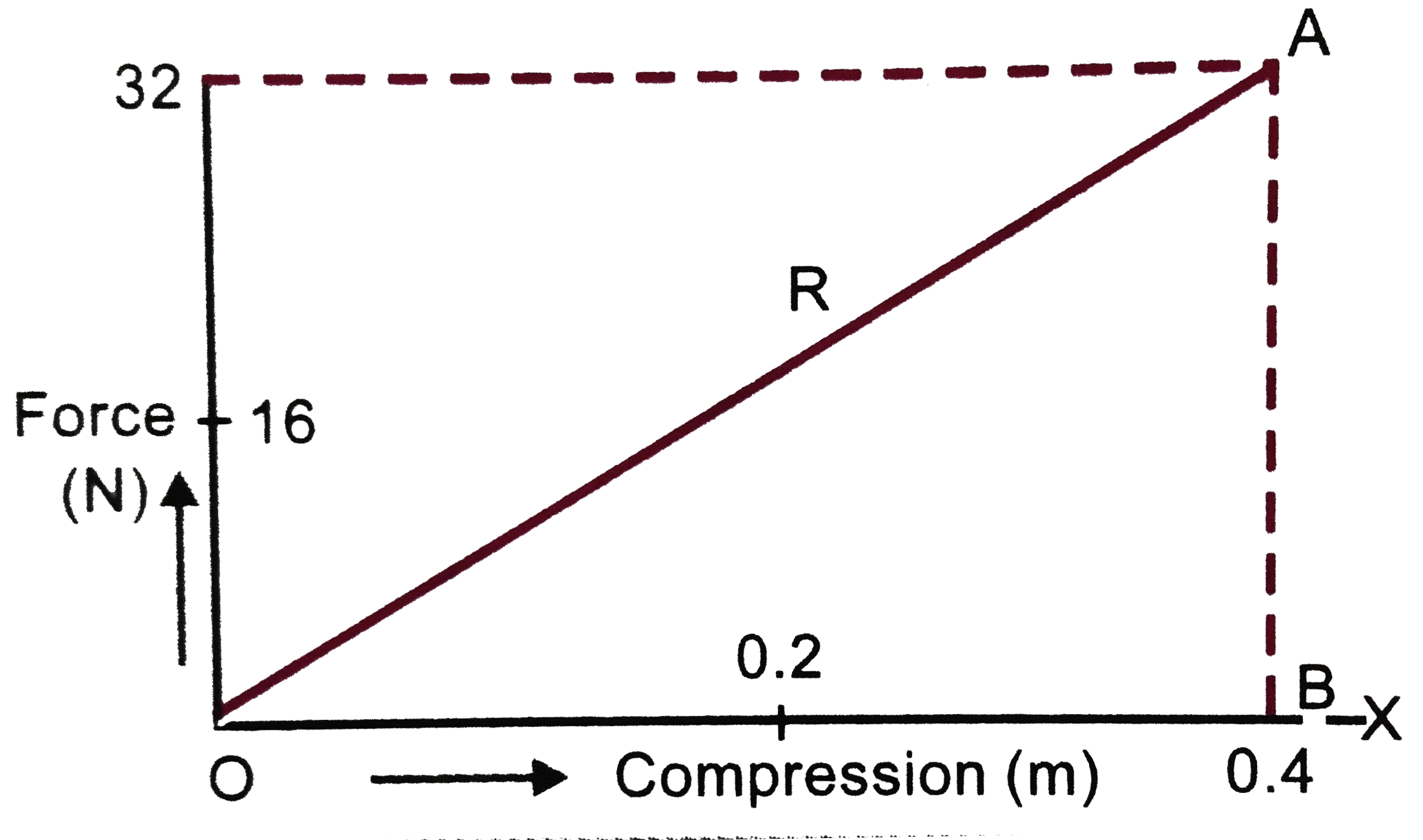 View Solution
View SolutionA body of mass 16 kg is made to oscillate on a spring of force constant 100Nkg−1. Deduce the angular frequency.
View SolutionA body of mass 1 kg oscillates on a spring of force constant 16 N/m. Calculate the angular frequency.
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
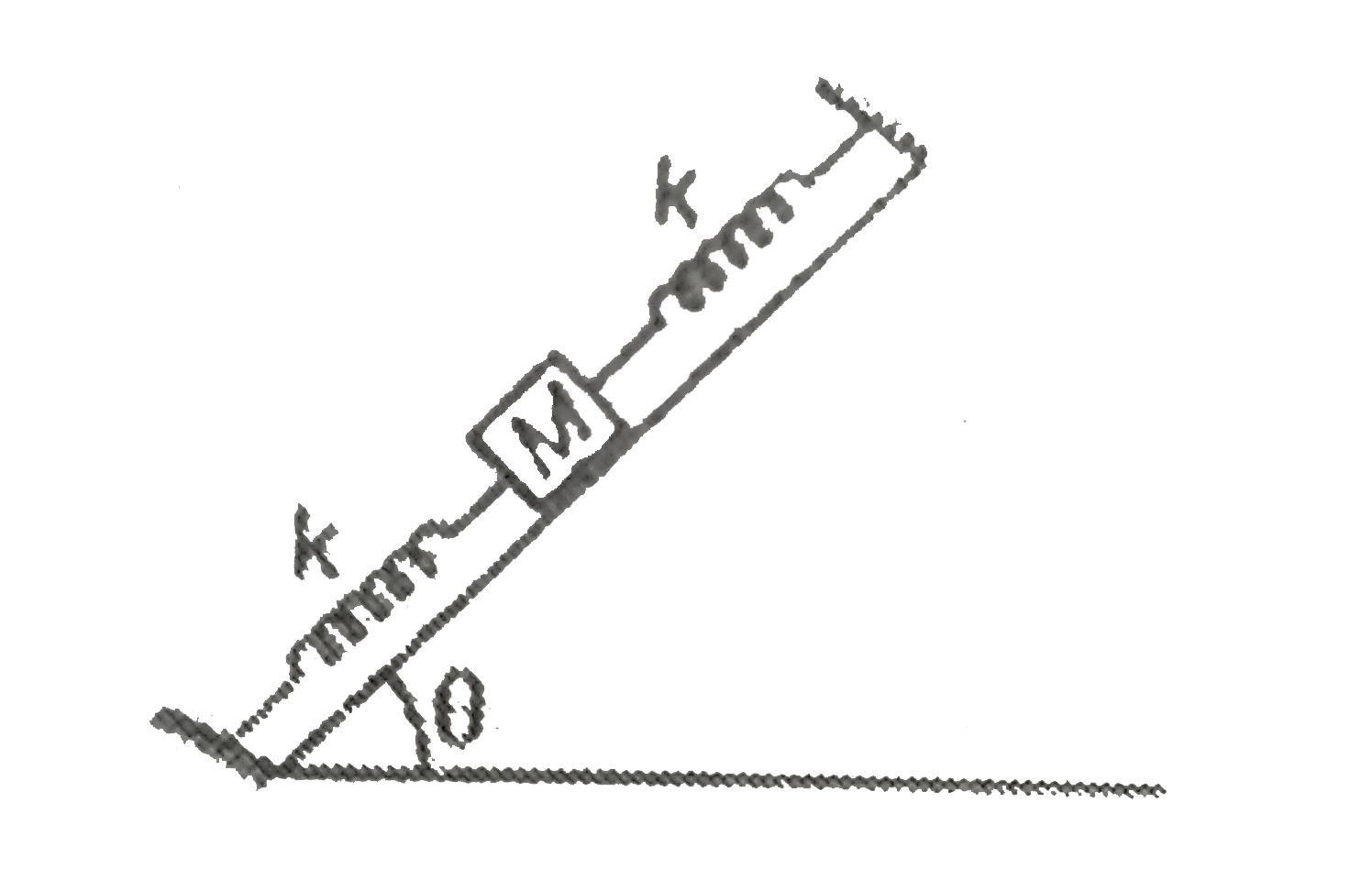 View Solution
View Solution

