A small trolley of mass 2.0kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation at a speed of 360 rpm,, the length of the stretched spring is 43cm. If the original length of the spring is 36cm, determing the force constant of the spring.
Here, m=2.0kg,v=36060=6rps
Extension produced in spring ,
y=43−36=7cm=7×10−2m
When turn table is set into rotation, the tension in the spring will provide the required centripetal force i.e., ky=mr(2πv)2=4π2v2mr
[where r is the length of stretched spring=43cm]
or k=4π2v2mry
=4×(22/7)2×62×(2.0)×(43×10−2)(7×10−2)
=17475Nm−1
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - conceptual problems84videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions99videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION2videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
A small trolley of mass 2.0 kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation at a speed of 300 rpm, the length of the stretched spring is 40 cm. If the original length of the spring is 35 cm, determine the force constant of the spring.
View SolutionA small trolley of mass 2.0kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation a speed of 600rpm, the length of stretched spring is 50cm. If the original length of the spring is 42cm, find the force constant of the spring.
View Solution
Knowledge Check
- Question 1 - Select One or More
Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this process - Question 2 - Select One
A body of mass m is tied to one end of a spring and whirled round in a horizontal circle with a constant angular velocity .The elongation is 1 cm . If the angular velocity is doubled , the elongation in the spring is 5 cm. what is the original length of the spring ?
A13 cmB14 cmC15 cmD16 cm - Question 3 - Select One
When a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
A4×10−2B4×10−3C8×10−2D8×10−3
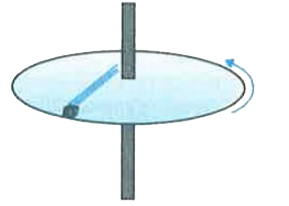
A small block of mass 1 kg is placed on a horizontal table, connected by a weightless spring to the central rod of the table as shown in the adjoining figure.
the table is set to rotate at a speed of 200 rpm which causes spring to stretch by 5 cm. If the original length of the spring is 30 cm, determine its force constant.
 View Solution
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
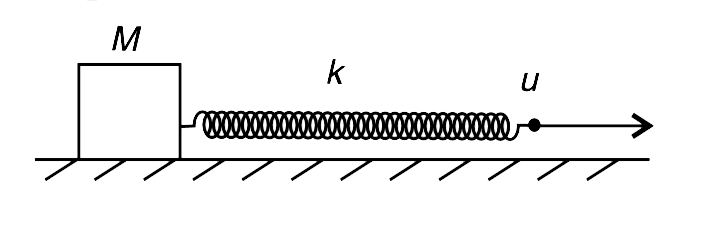
View SolutionA block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (x0) in the spring during the subsequent motion.
 View Solution
View SolutionA 4-kg block extends a spring by 16 cm from its unstretched postion .The block is removed and a 0.5 -kg boby is hung from the same spring If the spring is then stretched and released , what is the time period of oscillations of the mass suspendrd ? What is the force constant of the spring ?
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View Solution

