Explain the oscillations of a loaded spring and find the realtions for the time period and frequency in case of (i) horizontal spring (ii) vertical spring.
To explain the oscillations of a loaded spring and derive the relations for the time period and frequency for both horizontal and vertical springs, we can follow these steps:
Step 1: Understanding Oscillations of a Loaded Spring
A loaded spring executes Simple Harmonic Motion (SHM) when it is displaced from its equilibrium position. The restoring force acting on the spring is proportional to the displacement from the equilibrium position and is given by Hooke's Law:
F=−k⋅y
where:
- F is the restoring force,
- k is the spring constant,
- y is the extension or compression of the spring.
Step 2: Horizontal Spring Oscillations
1. Setup: Consider a horizontal spring fixed at one end with a mass M attached to the other end.
2. Displacement: When the mass is displaced by a distance y and released, it will oscillate back and forth.
3. Force Analysis: The force acting on the mass when displaced is:
F=−k⋅y
4. Time Period Derivation: The time period T for a mass-spring system executing SHM is given by:
T=2π√Mk
5. Frequency Relation: The frequency f is the reciprocal of the time period:
f=1T=12π√kM
Step 3: Vertical Spring Oscillations
1. Setup: Consider a vertical spring suspended from a fixed point with a mass M attached to it.
2. Equilibrium Position: The spring stretches under the weight of the mass until it reaches a new equilibrium position. Let the extension due to the weight be L1.
3. Force Analysis: At equilibrium, the weight of the mass balances the spring force:
Mg=k⋅L1
When the mass is further displaced by y, the restoring force becomes:
F=−k⋅(L1+y)+Mg=−k⋅y
4. Time Period Derivation: The time period for the vertical spring is given by:
T=2π√L1g
where g is the acceleration due to gravity.
5. Frequency Relation: The frequency f for the vertical spring is:
f=1T=12π√gL1
Summary of Relations
- Horizontal Spring:
- Time Period: T=2π√Mk
- Frequency: f=12π√kM
- Vertical Spring:
- Time Period: T=2π√L1g
- Frequency: f=12π√gL1
A loaded spring executes Simple Harmonic Motion (SHM) when it is displaced from its equilibrium position. The restoring force acting on the spring is proportional to the displacement from the equilibrium position and is given by Hooke's Law:
F=−k⋅y
where:
- F is the restoring force,
- k is the spring constant,
- y is the extension or compression of the spring.
1. Setup: Consider a horizontal spring fixed at one end with a mass M attached to the other end.
2. Displacement: When the mass is displaced by a distance y and released, it will oscillate back and forth.
3. Force Analysis: The force acting on the mass when displaced is:
F=−k⋅y
4. Time Period Derivation: The time period T for a mass-spring system executing SHM is given by:
T=2π√Mk
5. Frequency Relation: The frequency f is the reciprocal of the time period:
f=1T=12π√kM
1. Setup: Consider a vertical spring suspended from a fixed point with a mass M attached to it.
2. Equilibrium Position: The spring stretches under the weight of the mass until it reaches a new equilibrium position. Let the extension due to the weight be L1.
3. Force Analysis: At equilibrium, the weight of the mass balances the spring force:
Mg=k⋅L1
When the mass is further displaced by y, the restoring force becomes:
F=−k⋅(L1+y)+Mg=−k⋅y
4. Time Period Derivation: The time period for the vertical spring is given by:
T=2π√L1g
where g is the acceleration due to gravity.
5. Frequency Relation: The frequency f for the vertical spring is:
f=1T=12π√gL1
- Horizontal Spring:
- Time Period: T=2π√Mk
- Frequency: f=12π√kM
- Time Period: T=2π√L1g
- Frequency: f=12π√gL1
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions33videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions20videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions99videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
The frequency of oscillation of the springs shown in the figure will be
 A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2) - Question 2 - Select One
The frequency of oscillation of the spring shown in the figure will be
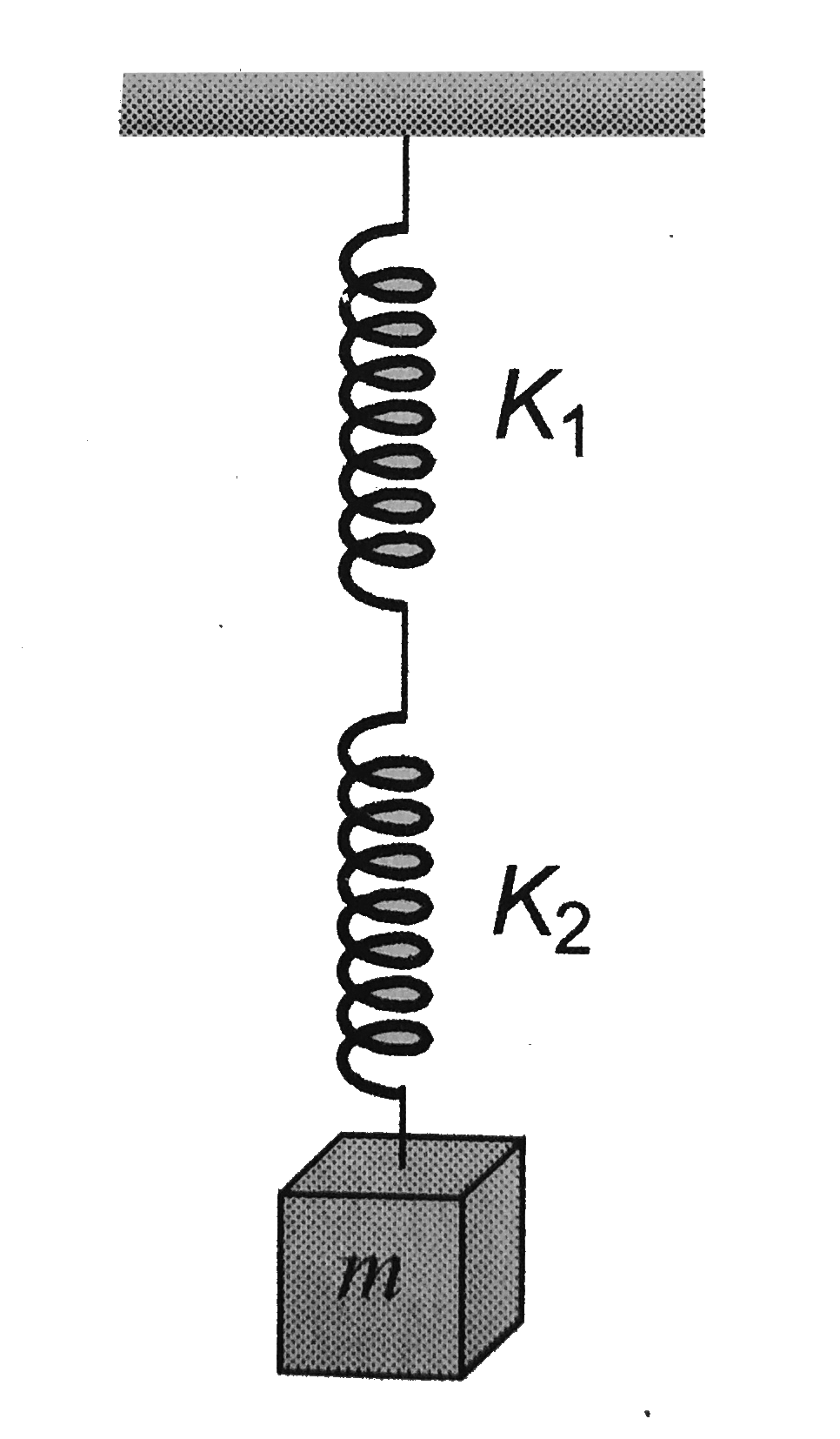 A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2))
A12π√KmB12π√(K1+K2)mK1K2C2π√KmD12π ⎷(K1K2m(K1+K2)) - Question 3 - Select One
The time period of a loaded spring on earth is 6s. On the surface of moon, the time period of the same loaded spring will be
A√6sB6√6sC1sD6s

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionWhat will be the change in time period of a loaded spring, when taken to moon ?
View SolutionThe period of oscillation of a spring pendulum is T. If the spring is cut into four equal parts, then find the time period corresponding to each part.
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now
View SolutionIn a spring block system if length of the spring is increased by 4%, then time period
View Solution

