A particle is performing simple harmonic motion of period T about a point O and it passes through a point P, where OP=y with velicity v in the direction →OP. Show that the time which elapses before it returns to P again is
(T/π)tan−1(vT2πy)
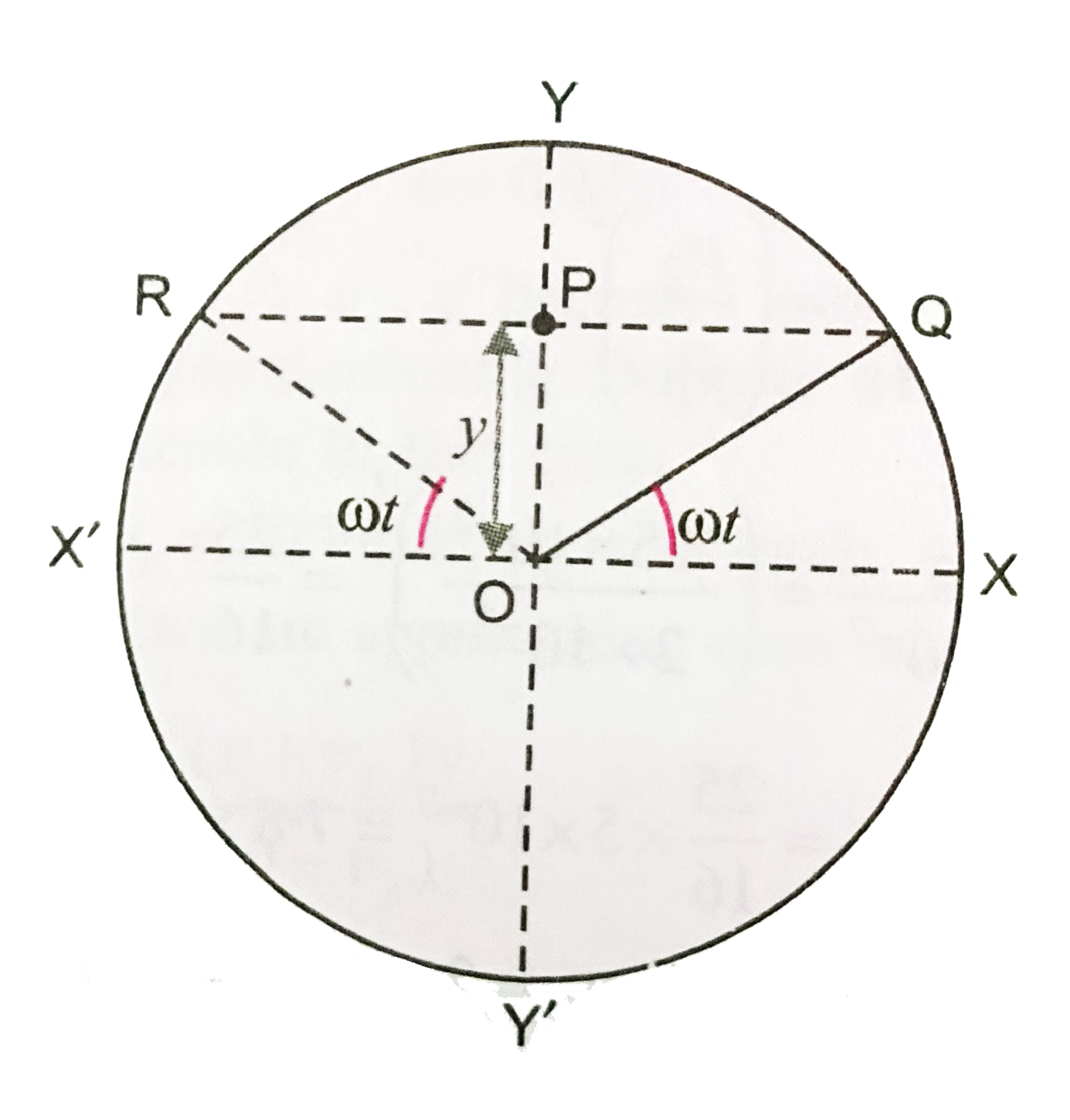
let Q and R be the positions of particle of reference on the circle of reference, corresponding to vibrating point at P in SHM, in the first instant and when it returns to p again.
Here, y=rsinωt
Velocity, v=dydtrωcosωt
∴yv=1ωtanωtortanωt=ωyv
or ωt=tan1(ωyv)
Required time, t=∠QOPω=2(90∘−ωt)ω
=2[90∘−tan−1(ωyv)]ω=2tan−1(vωy)ω
=2tan−1(vy×T2π)2π/T=Tπtan−1(vT2πy)proved
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS
19 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions
33 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A particle executes SHM with period T about a point O. It passes through a point P with velocity V along OP. Show that the time that elapses when it again comes to P is given by t=(Tπ)tan−(TV)2π.OP
View SolutionA particle performs simple harmonic motion about O with amolitude A and time period T. The magnitude of its acceleration at t=T8s after the particle reaches the extreme position would be
View Solution
Knowledge Check
A particle performs simple harmonic motion about O with amplitude A and time period T. The magnitude of its acceleration at t=T8s after the particle reaches the extreme position would be
A4π2A√2T2B4π2AT2C2π2A√2T2Dnone of theseA simple pendulum performs simple harmonic motion about x=0 with an amplitude a ans time period T. The speed of the pendulum at x=a2 will be
Aπa√32TBπaTC3π2aTDπa√3TA particle executes simple harmonic motion with a period of 16s. At time t=2s, the particle crosses the mean position while at t=4s, its velocity is 4ms−1 amplitude of motion in metre is
A√2πB16√2πC24√2πD32√2π
A simple pendulum performs simple harmonic motion about x=0 with an amplitude a ans time period T. The speed of the pendulum at x=a2 will be
View SolutionA particle executes simple harmonic motion with a period of 16s. At time t=2s, the particle crosses the mean position while at t=4s, its velocity is 4ms−1 amplitude of motion in metre is
View SolutionA particle is executing simple harmonic motion with a period of T seconds and amplitude a metre . The shortest time it takes to reach a point a√2 from its mean position in seconds is
View SolutionA particle is performing harmonic motion if its velocity are v1 and v2 at the displecement from the mean position are y1 and y2 respectively then its time period is
View SolutionA particle is executing simple harmonic motion with a period of T seconds and amplitude a metre. The shortest time it takes to reach α√2 point m from its mean position in seconds is
View Solution
