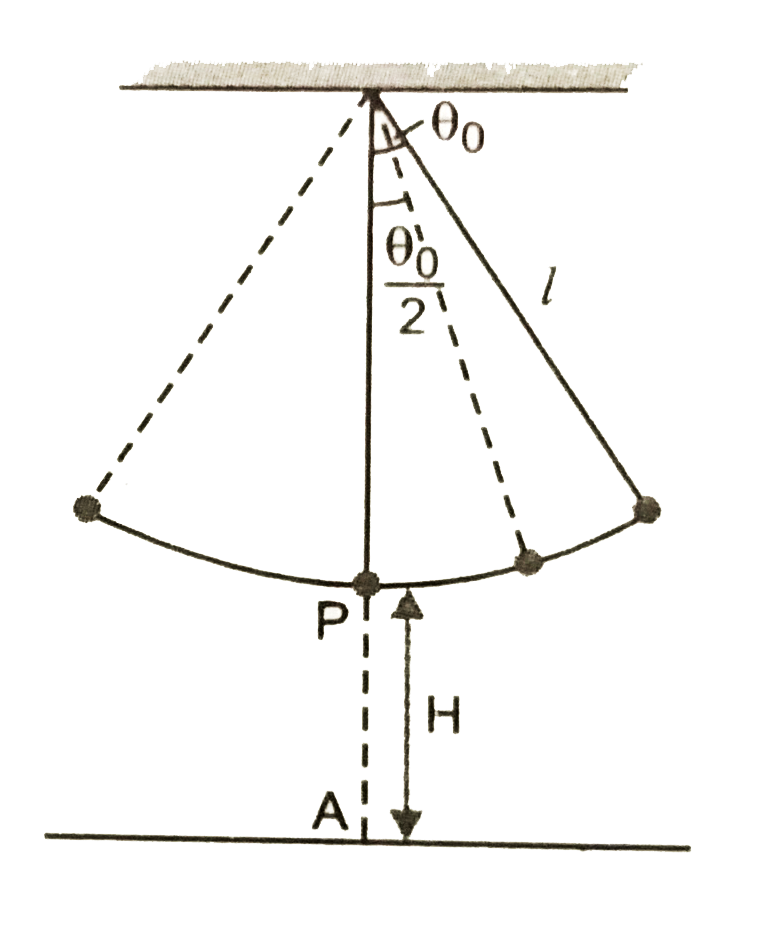
A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is $θ_{0}$ the string snaps at $0 = θ_{0} / 2 .$ Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume $θ_{0}$ to be small, so that ${sin θ}_{0} \approx θ_{0} and {cos θ}_{0} \approx 1 .$

Video Solution

Text Solution

Verified by Experts

Here, $θ_{0}$ is the angular amplitude of simple pendulum and time period, $T = 1 s$ . The angular displacement of the bob of the pendulum at any inisant t is given by
$θ = θ_{0} sin ω t = θ_{0} sin (\frac{2 π}{T}) t$
$= θ_{0} sin (\frac{2 π}{1}) t = θ_{0} sin 2 π t$ ..(i)
$(∵ T = 1 s .)$
At time $t_{1}$ , let $θ = θ_{0} / 2$ then from (i), we have
$\frac{θ_{0}}{2} = θ_{0} sin 2 π t_{1}$ or $2 π t_{1} = \frac{π}{6} or t_{1} = \frac{1}{12} s$
Differentiating (i) w.r.t. t, we have
$\frac{d θ}{d t} = 2 π θ_{0} cos 2 π t$
When $t = t_{1} = \frac{1}{12},$ then $\frac{d θ}{d t} = 2 π t h e t_{0} cos 2 π \times \frac{1}{12} = 2 π θ_{0} \times \frac{\sqrt{3}}{2} = \sqrt{3} π θ_{0}$
Angular velocity of the bob of simple pendulum is $ω = \frac{d θ}{d t} = \sqrt{3} π θ_{0}$
velocity of the bob of simple pendulum, $v = r ω = l ω = l (\sqrt{3} π θ_{0})$
It is acting perpendicular to string.
The vertical component velocity of bob, $v_{y} = v sin (θ_{0} / 2) = l \sqrt{3} π θ_{0} sin (θ_{0} / 2)$
Horizontal component velocity of bob, $v_{x} = v cos (θ_{0} / 2) = l \sqrt{3} π θ_{0} cos (θ_{0} / 2)$
The height of the bob when the pendulum snaps is , $H^{'} + H + l cos (θ_{0} / 2) = H + l [1 - cos (θ_{0} / 2)]$
If $t'$ is the time taken by the bob to fall through height $H (')$ , then using the relation , $S = u t + \frac{1}{2} a t^{2}$ ,
we have $s = H^{'}, u^{'} = v_{y} = l \sqrt{3} π θ_{0} sin (θ_{0} / 2), t = ?$
$∴ H^{'} = [\sqrt{3} π θ_{0} l sin (θ_{0} / 2)] t + \frac{1}{2} g t^{2}$
or $t^{2} + [\frac{2 \sqrt{3} π θ_{0} l sin (θ_{0} / 2)}{g}] t - \frac{2 H^{'}}{g} = 0$
$∴ t = \frac{- [\frac{2 \sqrt{3} θ_{0} l sin (θ_{0} / 2)}{g}] \pm \sqrt{[\frac{12 π^{2} θ_{0}^{2} l^{2} {sin}^{2} (θ_{0} / 2)}{g^{2}}] + 4 \times 2 H^{'} l g}}{2}$
$= \frac{- [\sqrt{3} π θ_{0} l sin (θ_{0} / 2)] \pm \sqrt{3 π^{2} θ_{0}^{2} l^{2} {sin}^{2} (θ_{0} / 2) + 2 H^{'} g}}{g}$
$= \frac{- \sqrt{3} π (θ_{0} / 2) \pm \sqrt{3 π^{2} θ_{0}^{2} (θ_{0}^{2} / 4) + 2 H^{'} g}}{g}$
As $θ_{0}$ is small so the terms with $θ_{0}^{2}$ beign very very small can be neglected.
$∴ t = \frac{\sqrt{2 H^{'} g}}{g} = \sqrt{\frac{2 H^{'}}{g}}$
Now, $H^{'} = H + l - l \times l = H$ $[∵ cos (θ_{0} / 2) = 1]$
$∴ t = \sqrt{\frac{2 H^{'}}{g}} = \sqrt{\frac{2 H}{g}}$
The horizontal distance travelled by bob after snapping
$x = v_{x} t = [\sqrt{3} l π θ_{0} cos (θ_{0} / 2)] \sqrt{\frac{2 H}{g}} = \sqrt{3} l π θ_{0} \times 1 \times \sqrt{2 H / g} = \sqrt{\frac{6 H}{g}} \times θ_{0} l π$ j
At the time of snapping, the horizontal distance of the bob from point A is $= l sin (θ_{0} / 2) = l θ_{0} / 2$
Thus the distance of bob from A where it meets the ground is
$= \frac{l θ_{0}}{2} - \sqrt{\frac{6 H}{g}} l π θ_{0} = l θ_{0} [\frac{1}{2} - π \sqrt{\frac{6 H}{g}}$

Updated on:21/07/2023