Assertion : If the length of the simple pendulum is equal to the radius of the earth, the period of the pendulum is T=2π√R/g
Reason : Length of this pendulum is equal to radius of earth.
both, Assertion and Reason are true and Reason is the correct explanation of the Assertion.
both, Assertion and Reason are true but Reason is not a correct explanation of the Assertion.
Assertion is flase but the Reason is true.
both,Assertion and Reason are false.
The correct Answer is:C
Here, Assertion is wrong, because for a pendulum of large length L1, the time period is given by
T=2π√R(1+Re/Re)g
whereRe= radius of earth.
When, L=Re,
then T=2π√Re(1+Re/Re)g=2π√Re2g
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions13videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question8videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
If the length of a simple pendulum is equal to the radius of the earth, its time period will be
A2π√R/gB2π√R/2gC2π√2R/gDinfinite - Question 2 - Select One
The time period of a simple pendulum at the centre of the earth is
AzeroBinfiniteCless than zeroDtwo second - Question 3 - Select One
When the length of the pendulum increases, the time period of the pendulum ______.
AincreasesBdecreasesCBoth a and bDNone of these.
When the length of the pendulum increases, the time period of the pendulum ______.
View SolutionFor infinitely long length of the pendulum, the time period of the pendulum is
View SolutionAssertion : The length of a simple pendulum is increases by 4% the corresponding decrease in time period will be 2%
Reason : T=∝√1View SolutionThe l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
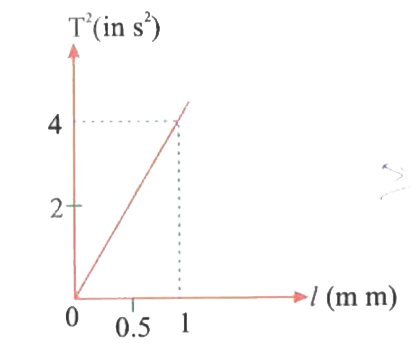 View Solution
View SolutionWhen the length of the pendulum increases, the time period of the pendulum ______.
View Solution

