A hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
To find the magnetic field induction at a point inside a hollow cylindrical conductor at a distance r (where a<r<b), we can follow these steps:
Step 1: Understand the Geometry of the Problem
We have a hollow cylindrical conductor with an inner radius a and an outer radius b. The current I is uniformly distributed across its cross-section. We need to find the magnetic field at a distance r from the axis of the cylinder, where a<r<b.
Hint: Visualize the hollow cylinder and identify the regions: the inner radius a and the outer radius b.
Step 2: Calculate the Area of the Cross-section
The total cross-sectional area of the hollow cylinder is given by:
A=πb2−πa2=π(b2−a2)
Hint: Use the formula for the area of a circle to find the area of the hollow part.
Step 3: Determine the Current Density
The current density J (current per unit area) is given by:
J=IArea=Iπ(b2−a2)
Hint: Remember that current density is the total current divided by the cross-sectional area.
Step 4: Calculate the Current Enclosed by the Radius r
The area of the cross-section up to radius r is:
Ar=πr2−πa2=π(r2−a2)
The current Ir enclosed within this area is:
Ir=J⋅Ar=Iπ(b2−a2)⋅π(r2−a2)=I(r2−a2)b2−a2
Hint: Use the current density to find the current enclosed within the radius r.
Step 5: Apply Ampère's Law
According to Ampère's Law, the magnetic field B around a circular path of radius r is given by:
B⋅2πr=μ0Ir
Substituting Ir:
B⋅2πr=μ0(I(r2−a2)b2−a2)
Hint: Remember that the path length for the circular loop is 2πr.
Step 6: Solve for the Magnetic Field B
Rearranging the equation gives:
B=μ0I(r2−a2)2πr(b2−a2)
Hint: Isolate B to find the expression for the magnetic field induction.
Final Expression
Thus, the magnetic field induction at a distance r from the axis of the hollow cylindrical conductor is:
B=μ0I(r2−a2)2πr(b2−a2)
We have a hollow cylindrical conductor with an inner radius a and an outer radius b. The current I is uniformly distributed across its cross-section. We need to find the magnetic field at a distance r from the axis of the cylinder, where a<r<b.
The total cross-sectional area of the hollow cylinder is given by:
A=πb2−πa2=π(b2−a2)
The current density J (current per unit area) is given by:
J=IArea=Iπ(b2−a2)
The area of the cross-section up to radius r is:
Ar=πr2−πa2=π(r2−a2)
The current Ir enclosed within this area is:
Ir=J⋅Ar=Iπ(b2−a2)⋅π(r2−a2)=I(r2−a2)b2−a2
According to Ampère's Law, the magnetic field B around a circular path of radius r is given by:
B⋅2πr=μ0Ir
Substituting Ir:
B⋅2πr=μ0(I(r2−a2)b2−a2)
Rearranging the equation gives:
B=μ0I(r2−a2)2πr(b2−a2)
Thus, the magnetic field induction at a distance r from the axis of the hollow cylindrical conductor is:
B=μ0I(r2−a2)2πr(b2−a2)
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A hollow cylindrical conductor of radii a and b carries a current I uniformly spread over its cross-section. Prove that the magnetic field induction B for point inside the body of the conductor at a distance r from the axis of cylinder is given by, B=μ0μrI(r2−a2)2π(b2−a2)r
View SolutionFigure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a<r<b) is given by. B=μ0i2π(b2−a2)r2−a2r.Check this formula for the limiting case of a=0.
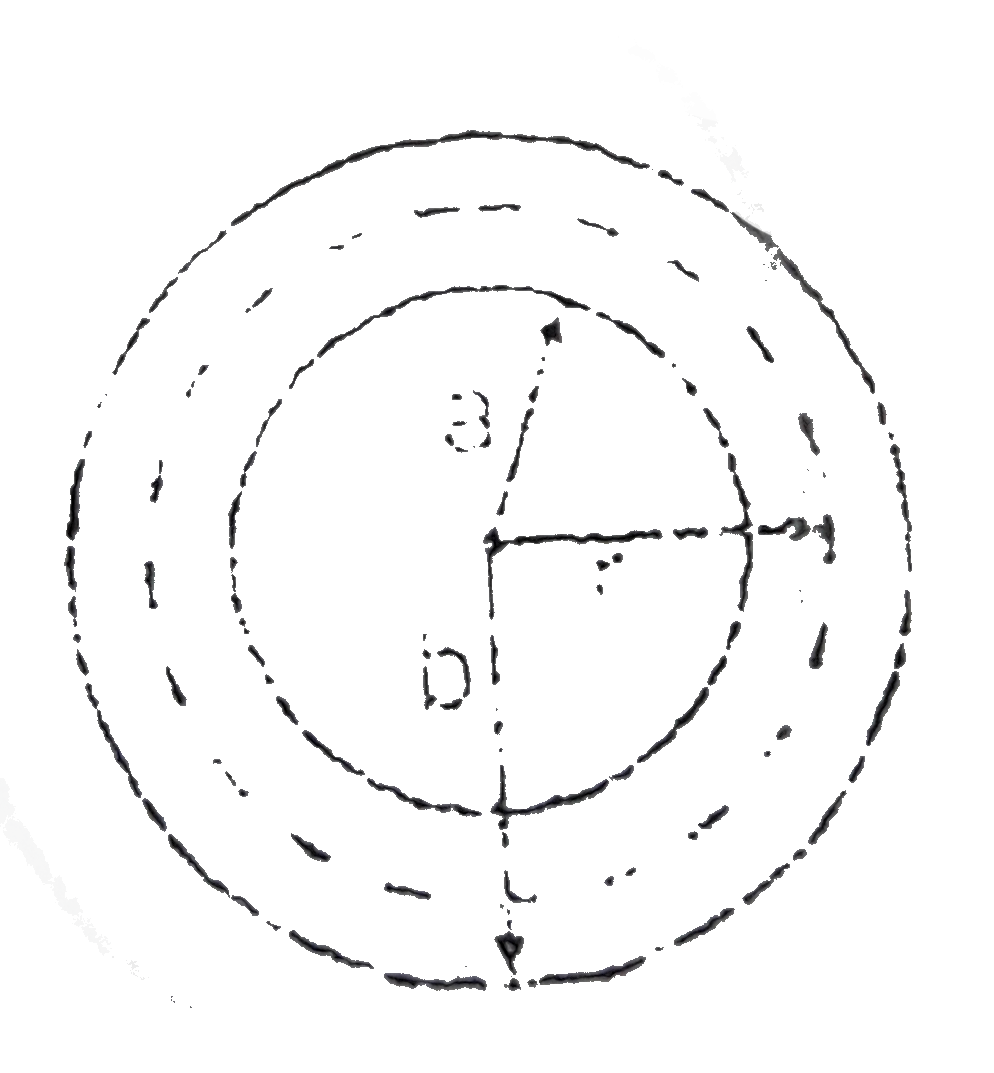
View Solution
Knowledge Check
Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
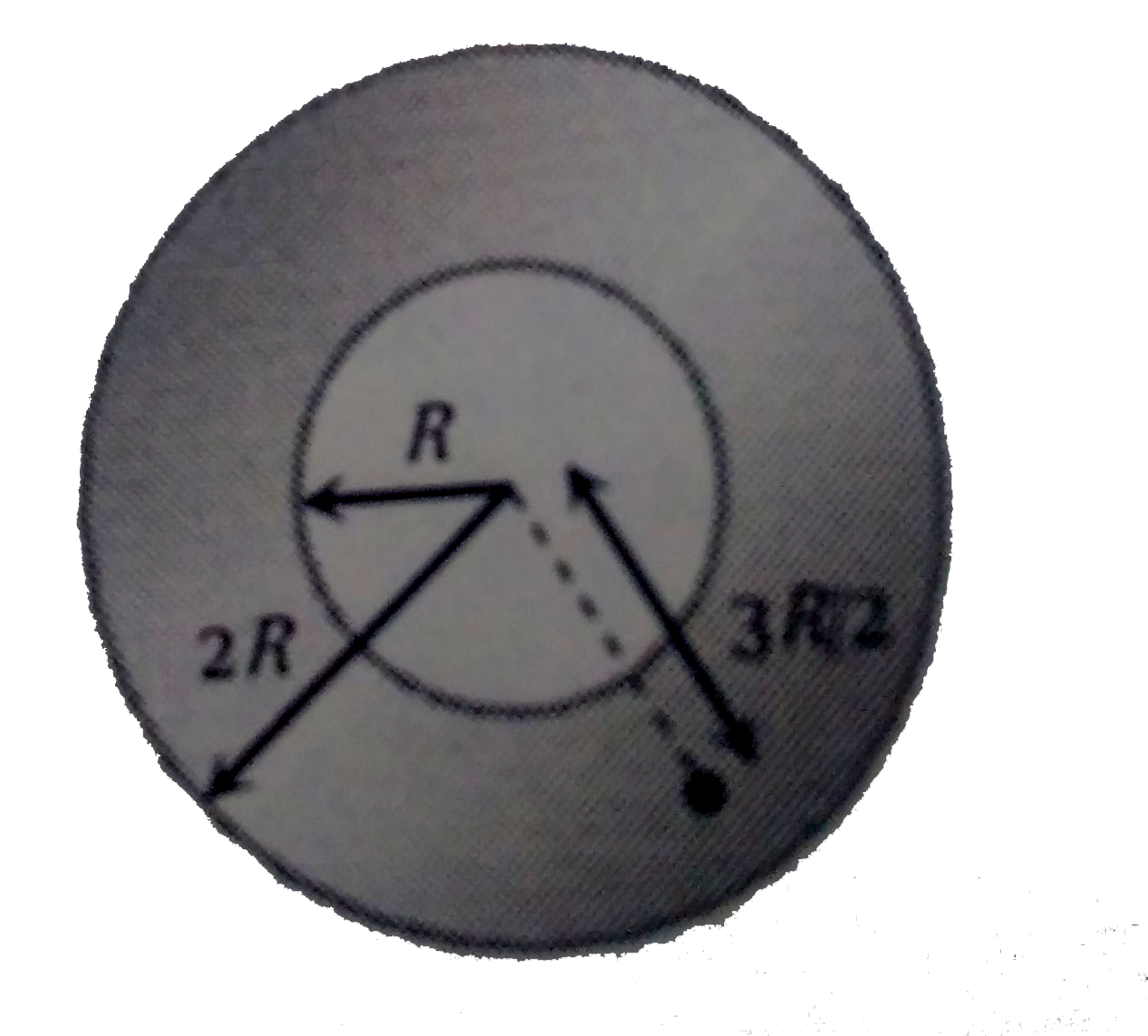 AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πR
AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πR
A long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA long straight solid metal rod of radius 4cm carries a current 2A, uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 3cm from the axis of the wire.
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionA long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View SolutionA long straight solid conductor of radius 6cm carries a current of 8A, which uniformly distributed over its circular cross-section. Find the magnetic field (a) at a distance of 3cm from the axis of the conductor (b) at a distance 10cm from the axis of the conductor.
View SolutionA long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long straight solid conductor of radius 5cm carries a current of 3A, which is uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 4cm from the axis of the conductor. Relative permeability of the conductor=1000.
View Solution
