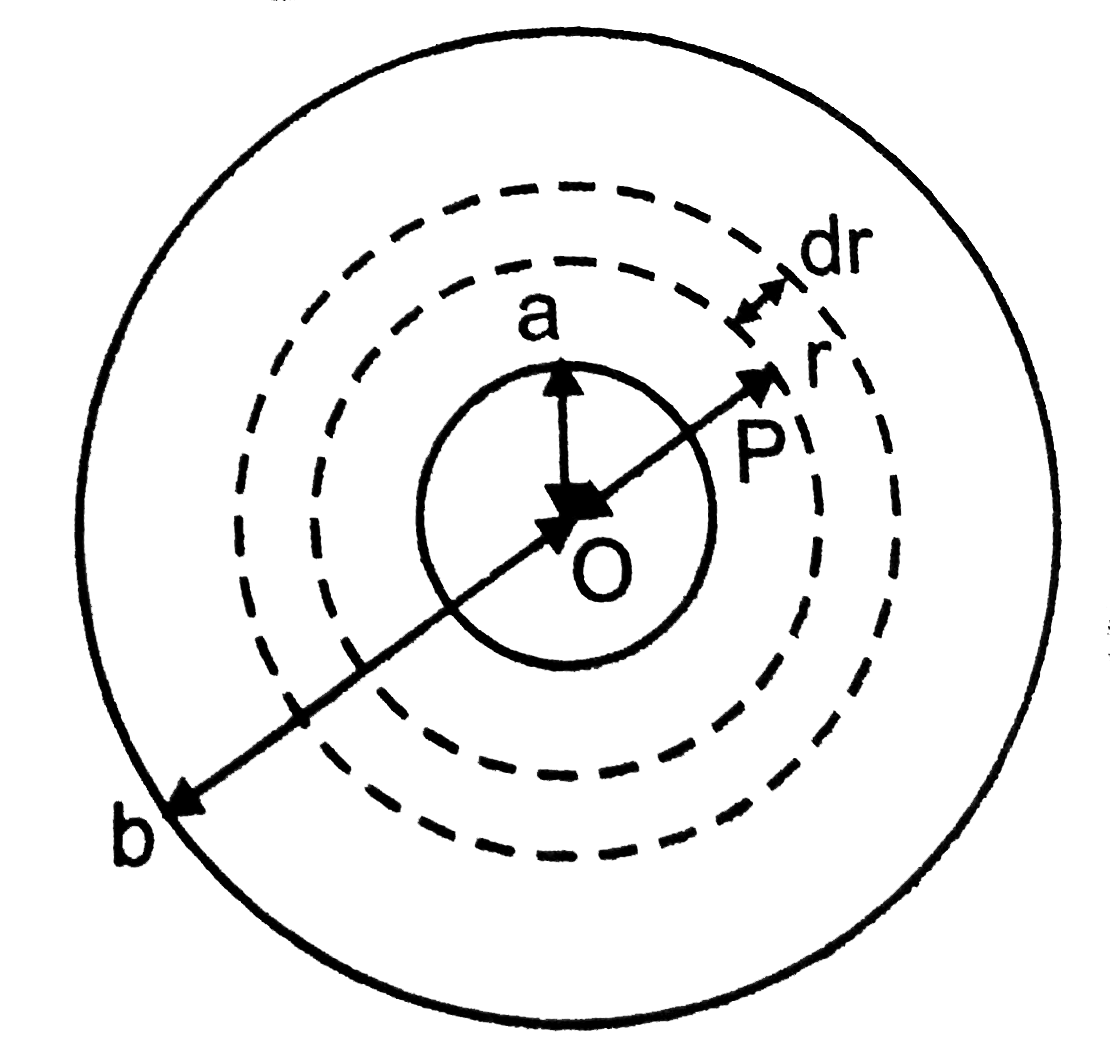
A hollow cylindrical conductor of radii a and b carries a current I uniformly spread over its cross-section. Prove that the magnetic field induction B for point inside the body of the conductor at a distance r from the axis of cylinder is given by, $B = \frac{μ_{0} μ_{r} I (r^{2} - a^{2})}{2 π (b^{2} - a^{2}) r}$

Video Solution

Text Solution

Verified by Experts

Let P be a point at a perpendicular distance r from the axis of the cylindrical conductor. Due to current I through cylinder a magnetic field is set up perpendicular to the length of cylinder, which is in the form of concentric magnetic lines of force whose centre lies on the axis of cylinder. Consider an elementary co-axical cylinderical layer of cylinder of radius r and thickness dr as shown in figure. Current through the cylinder of inner radius a and outer radius r is
$I^{'} = \frac{I}{π (b^{2} - a^{2})} π (r^{2} - a^{2}) = \frac{I (r^{2} - a^{2})}{(b^{2} - a^{2})}$
Using Ampere circuital law
$\oint \to B . d \to l = μ_{0} μ_{r} I^{'}$ or $B 2 π r = \frac{μ_{0} μ_{r} I (r^{2} - a^{2})}{(b^{2} - a^{2})}$ or $B = \frac{μ_{0} μ_{r} I}{2 π (b^{2} - a^{2})} \frac{(r^{2} - a^{2})}{r}$

Updated on:21/07/2023

Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
A $B = 0$ at the axis
B $B \propto x$ for $0 \leq x \leq r$
C $B \propto 1 / x$ for $x > r$
DB is maximum for $x = r$
A long, thick straight conductor of radius $R$ carries current $I$ uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance $R / 2$ from surface inside the conductor and outside the conductor is:
A $1 : 16$
B $1 : 1$
C $1 : 4$
D $9 / 16$