If a particle of charge q is moving with velocity v along the y-axis and the magnetic field B is acting along the z-axis, use the expression →F=q(→v×→B) to find the direction of the force →F acting on it.
To find the direction of the force →F acting on a charged particle moving in a magnetic field, we can use the expression →F=q(→v×→B). Here’s a step-by-step solution:
Step 1: Identify the vectors
- The velocity vector →v of the particle is along the y-axis. We can represent this as:
→v=v^j
where ^j is the unit vector in the y-direction.
- The magnetic field vector →B is acting along the z-axis. We can represent this as:
→B=B^k
where ^k is the unit vector in the z-direction.
Step 2: Calculate the cross product →v×→B
Using the right-hand rule for the cross product, we can determine the direction of →F:
→F=q(→v×→B)=q(v^j×B^k)
Step 3: Apply the right-hand rule
To find the direction of →F:
- Point your fingers in the direction of →v (upward along the y-axis).
- Curl your fingers in the direction of →B (outward along the z-axis).
- Your thumb will point in the direction of →F.
Step 4: Determine the direction of the force
Using the right-hand rule:
- The velocity →v is in the positive y-direction.
- The magnetic field →B is in the positive z-direction.
- Therefore, the force →F will be in the negative x-direction.
Final Result
Thus, the direction of the force →F acting on the particle is in the negative x-direction.
---
- The velocity vector →v of the particle is along the y-axis. We can represent this as:
→v=v^j
where ^j is the unit vector in the y-direction.
→B=B^k
where ^k is the unit vector in the z-direction.
Using the right-hand rule for the cross product, we can determine the direction of →F:
→F=q(→v×→B)=q(v^j×B^k)
To find the direction of →F:
- Point your fingers in the direction of →v (upward along the y-axis).
- Curl your fingers in the direction of →B (outward along the z-axis).
- Your thumb will point in the direction of →F.
Using the right-hand rule:
- The velocity →v is in the positive y-direction.
- The magnetic field →B is in the positive z-direction.
- Therefore, the force →F will be in the negative x-direction.
Thus, the direction of the force →F acting on the particle is in the negative x-direction.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Conceptual Problems (d)
Explore 2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Very Short Answer Questions (a)
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A magnetic of magnetic moment placed along the X-axis in an magnet field .Find the torque acting on the magnetic field
View SolutionThe force →F experienced by a particle of charge q moving with velocity →v in a magnetic field →B is given by →F=q(→v×→B) . Of these, name the pairs of vectors which are always at right angles to each other.
View Solution
Knowledge Check
An electric charge q is moving with a velocity w in the direction of a magnetic field B. The magnetic force acting on the charge is
AqvBBzeroCqvBDvqBA charged particle of charge q moving with the velocity v, enters along the axis of a solenoid carrying a current. If B is the magnetic induction along the axis of the solenoid then the force acting on the charged particle will be
AqvBBless then qvBCzeroDmore than qvBA charge q moves with a velocity 2m/s along x- axis in a unifrom magnetic field B=(ˆi+2ˆj+3ˆk) tesla.
ACharge will experience a force in z-y planeBCharge will experience a force along- y aixsCCharge will experience a force + z aixsDCharge will experience a force along - z axis
An electrons is moving along +ve x-axis in the presence of uniform magnetic field along +ve y-axis. What is the direction of the force acting on it?
View SolutionThe force acting on a charge 'q' moving with a velocity V in a magnetic field of induction B is given by
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
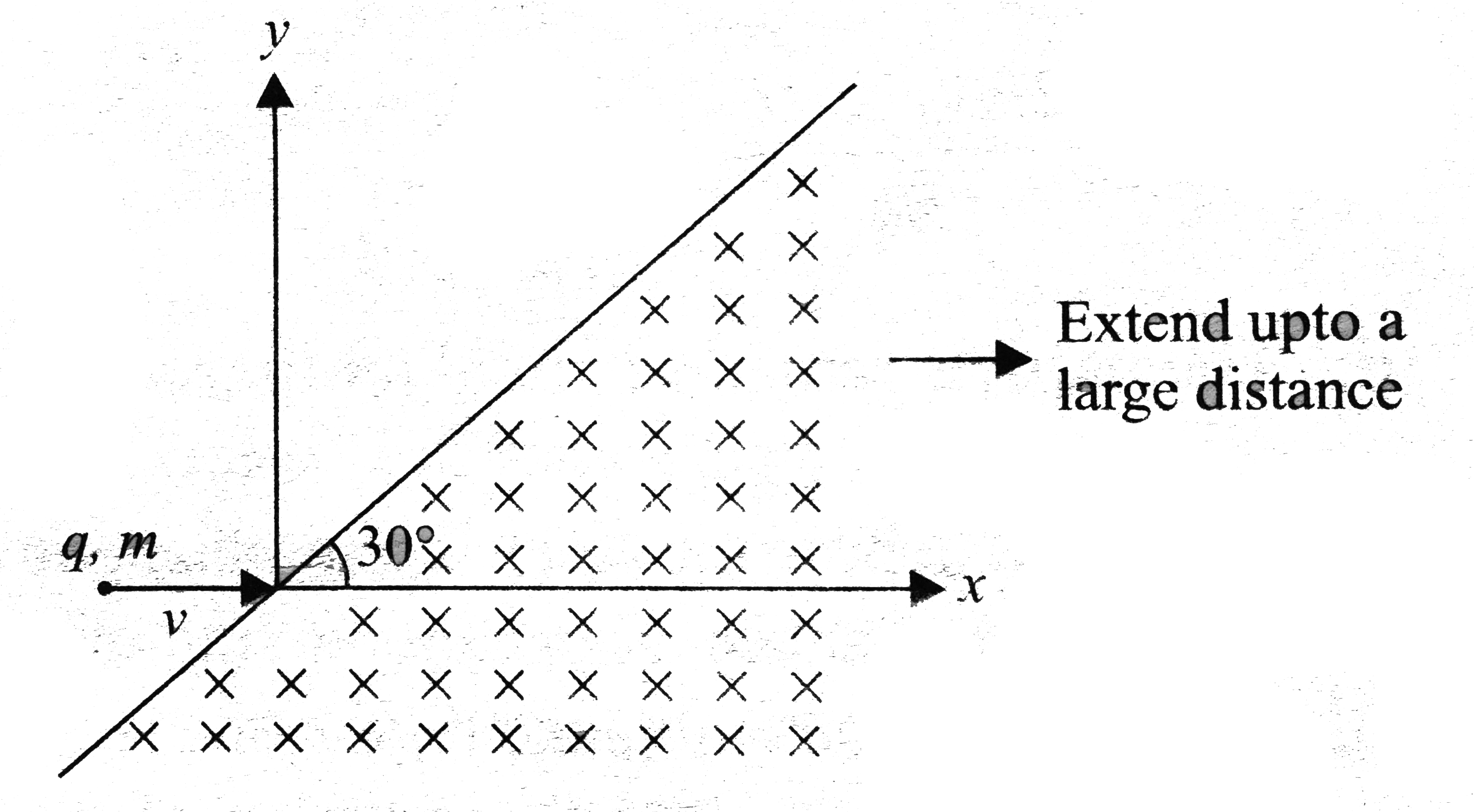
View SolutionThe force →F experienced by a particle of charge q moving with a velocity →v in a magnetic field →B is given by →F=q(→v×→B). Which pairs of vectors are at right angles to each other?
View Solution