An electrons is moving along +ve x-axis in the presence of uniform magnetic field along +ve y-axis. What is the direction of the force acting on it?
To determine the direction of the force acting on an electron moving along the positive x-axis in the presence of a uniform magnetic field along the positive y-axis, we can use the Lorentz force law, which states:
F=q(v×B)
Where:
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity vector,
- B is the magnetic field vector.
Step 1: Identify the velocity and magnetic field vectors
The electron is moving along the positive x-axis, so we can express the velocity vector as:
v=vx^i+0^j+0^k=vx^i
Where vx is the speed of the electron along the x-axis.
The magnetic field is along the positive y-axis, so we express the magnetic field vector as:
B=0^i+By^j+0^k=By^j
Step 2: Calculate the cross product v×B
Now we calculate the cross product v×B:
v×B=(vx^i)×(By^j)
Using the right-hand rule for the cross product, we can find:
^i×^j=^k
Thus,
v×B=vxBy^k
Step 3: Determine the force F
Now we substitute the charge of the electron (which is negative) into the Lorentz force equation:
F=q(v×B)=(−e)(vxBy^k)
Where e is the magnitude of the charge of the electron.
This results in:
F=−evxBy^k
Step 4: Analyze the direction of the force
Since the charge q is negative, the force F will be in the opposite direction of ^k:
F=−evxBy(−^k)=evxBy(−^k)
Thus, the force acting on the electron is in the negative z-direction.
Conclusion
The direction of the force acting on the electron is along the negative z-axis.
---
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity vector,
- B is the magnetic field vector.
The electron is moving along the positive x-axis, so we can express the velocity vector as:
v=vx^i+0^j+0^k=vx^i
Where vx is the speed of the electron along the x-axis.
B=0^i+By^j+0^k=By^j
Now we calculate the cross product v×B:
v×B=(vx^i)×(By^j)
^i×^j=^k
Thus,
v×B=vxBy^k
Now we substitute the charge of the electron (which is negative) into the Lorentz force equation:
F=q(v×B)=(−e)(vxBy^k)
Where e is the magnitude of the charge of the electron.
F=−evxBy^k
Since the charge q is negative, the force F will be in the opposite direction of ^k:
F=−evxBy(−^k)=evxBy(−^k)
Thus, the force acting on the electron is in the negative z-direction.
The direction of the force acting on the electron is along the negative z-axis.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-227videos
ELECTRODYNAMICS
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
Similar Questions
An electron in moving along positive x-axis in the presence of uniform magnetic field along positive y-axis. What is the direction of the force acting on it ?
View SolutionAn electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View Solution
Knowledge Check
- Question 1 - Select One
An electron is moving along positive x-axis A unifrom electric field exists towards negative y-axis. What should be the direction of magnetic field of suitable magnitude so that net force of electrons is zero .
APositive z-axisBNegative z-axisCPositive y-axisDNegative y-axis - Question 2 - Select One
An electron is moving along positive x-axis A unifrom electric filed exists to wards negative y-axis. What should be the direaction of magnetic field of suitable magnitude so that net force of electrons is zero .
Apositivez-axisBnegative z-axisCpositivey-axisDnegative y-axis - Question 3 - Select One
The strenght of magnetic field along the axis of a solenoid coil:
Aincrease on increasing current flowing through the solenoid coilBincrease on increasing the number of turns in the solenoid coilCincreases on introducing a soft iron core inside the solenoid coil .Dall to the above
An electron beam projected along +x axis, experience a force due to a magnetic field along the +y- axis. What is the direction of the magnetic field?
View SolutionAn electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View SolutionA beam of α-particle projected along +x - axis, experiences a force due to a magnetic field along the +y-axis. What is the direction of the magnetic field?
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
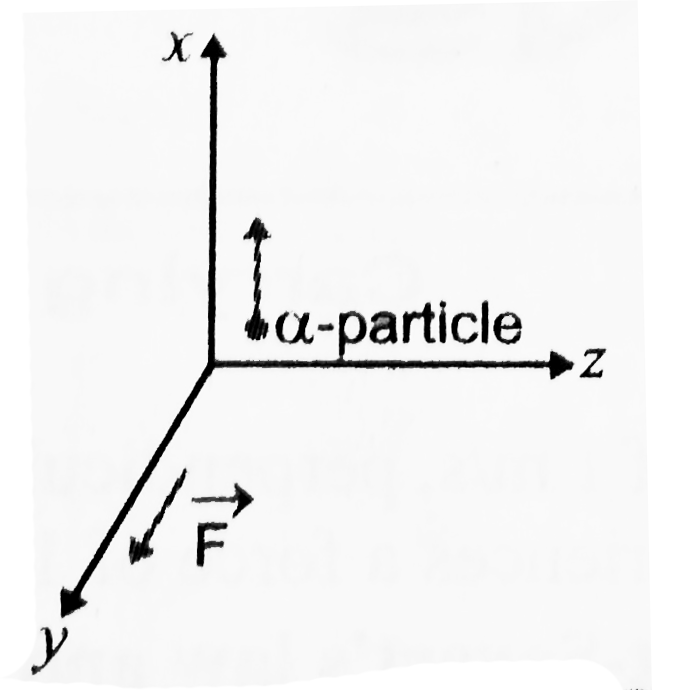 View Solution
View SolutionA charge q moving along the X-axis with a velocity →v is subjected to a uniform magnetic field B acting along the Z-axis as it crosses the origin O. Figure.
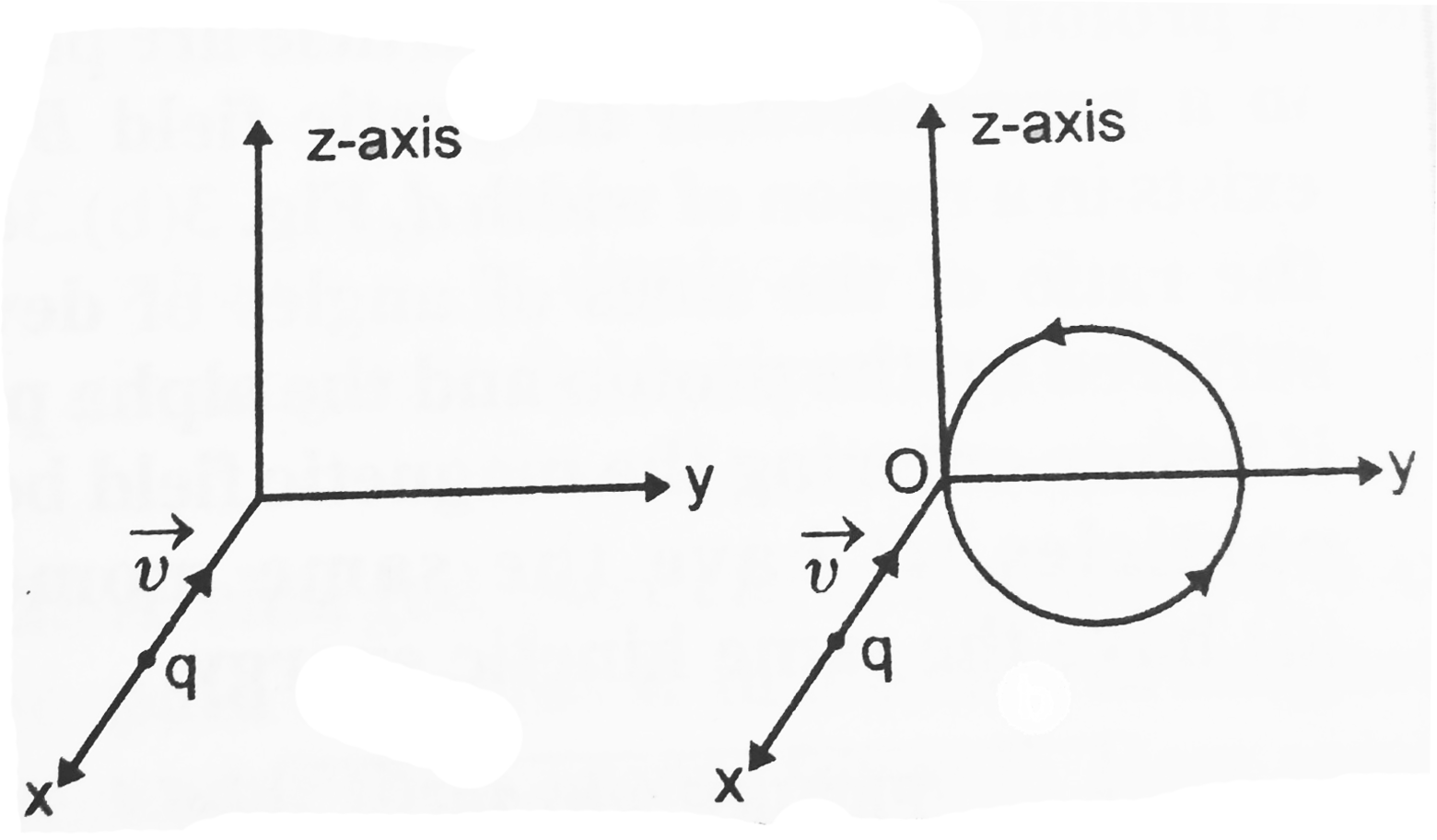
(i) Trace its trajectory . (ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify yous answer.View Solution

