A direct current I=10A flows in a long straight round conductor. Find the magnetic flux through a half of the wire's cross-section per one meter of its length.
To solve the problem of finding the magnetic flux through half of the wire's cross-section per one meter of its length when a direct current of I=10A flows in a long straight round conductor, we can follow these steps:
Step 1: Understand the Setup
We have a long straight round conductor with a radius r and a current I=10A flowing through it. We need to find the magnetic flux through half of the cross-section of the wire per one meter of its length.
Step 2: Use Ampere's Circuital Law
According to Ampere's Circuital Law, the magnetic field B around a long straight conductor can be calculated using the formula:
∮B⋅dl=μ0Ienc
For a circular path of radius r, this simplifies to:
B⋅2πr=μ0I
Thus, the magnetic field B at a distance r from the center of the wire is given by:
B=μ0I2πr
Step 3: Calculate the Magnetic Field
Substituting I=10A into the equation, we have:
B=μ0⋅102πr
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 4: Determine the Area for Flux Calculation
The magnetic flux ΦB through a surface is given by:
ΦB=∫B⋅dA
For half of the cross-section of the wire, we consider the area A of a semicircle:
A=12πr2
Step 5: Calculate the Magnetic Flux
To find the flux through half of the cross-section, we need to integrate the magnetic field over the area:
ΦB=∫r0B⋅dA
Since dA=rdθ for a circular area, we can express the area element in polar coordinates. However, for simplicity, we can use the average magnetic field over the area.
Using the average value of B over the semicircular area, we can calculate:
ΦB=B⋅A=(μ0⋅102πr)⋅(12πr2)
ΦB=μ0⋅10⋅r4
Step 6: Substitute μ0 and Calculate
Substituting μ0=4π×10−7T m/A:
ΦB=(4π×10−7)⋅10⋅r4=π×10−6⋅r
Step 7: Final Result
Thus, the magnetic flux through half of the wire's cross-section per one meter of its length is:
ΦB=π×10−6Weber
We have a long straight round conductor with a radius r and a current I=10A flowing through it. We need to find the magnetic flux through half of the cross-section of the wire per one meter of its length.
According to Ampere's Circuital Law, the magnetic field B around a long straight conductor can be calculated using the formula:
∮B⋅dl=μ0Ienc
For a circular path of radius r, this simplifies to:
B⋅2πr=μ0I
Thus, the magnetic field B at a distance r from the center of the wire is given by:
B=μ0I2πr
Substituting I=10A into the equation, we have:
B=μ0⋅102πr
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
The magnetic flux ΦB through a surface is given by:
ΦB=∫B⋅dA
For half of the cross-section of the wire, we consider the area A of a semicircle:
A=12πr2
To find the flux through half of the cross-section, we need to integrate the magnetic field over the area:
ΦB=∫r0B⋅dA
Since dA=rdθ for a circular area, we can express the area element in polar coordinates. However, for simplicity, we can use the average magnetic field over the area.
ΦB=B⋅A=(μ0⋅102πr)⋅(12πr2)
ΦB=μ0⋅10⋅r4
Substituting μ0=4π×10−7T m/A:
ΦB=(4π×10−7)⋅10⋅r4=π×10−6⋅r
Thus, the magnetic flux through half of the wire's cross-section per one meter of its length is:
ΦB=π×10−6Weber
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
A direct current I=10A a flows in a long straight round conductor. Find the magnetic flux through a half of wire's cross-section per one meter of its length.
View SolutionA direct current I flows in a long straight conductor whose cross section has the form of a thin halr-ring of radius R. The same current flows in the opposite direction along a thin conductor located on the axis of the first conductor. Find the magnetic induction froce between the given conductors reduced to a unit of their length.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
20 ampere current is flowing in a long straight wire. The intensity of magnetic field at a distance 10 cm from the wire will be
A4×10−5Wb/mB9×10−5Wb/mC8×10−5Wb/mD6×10−5Wb/m - Question 2 - Select One
A current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
A4μ0i√5πLBμ0i2πLCμ0i√2LDzero - Question 3 - Select One
A current of 4 A is flowing in a cylindrical conductor. The number of free electrons passing per second through the cross-section of conductor is
A2⋅1019B3⋅1020C2.5⋅1019D4⋅1018
A current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
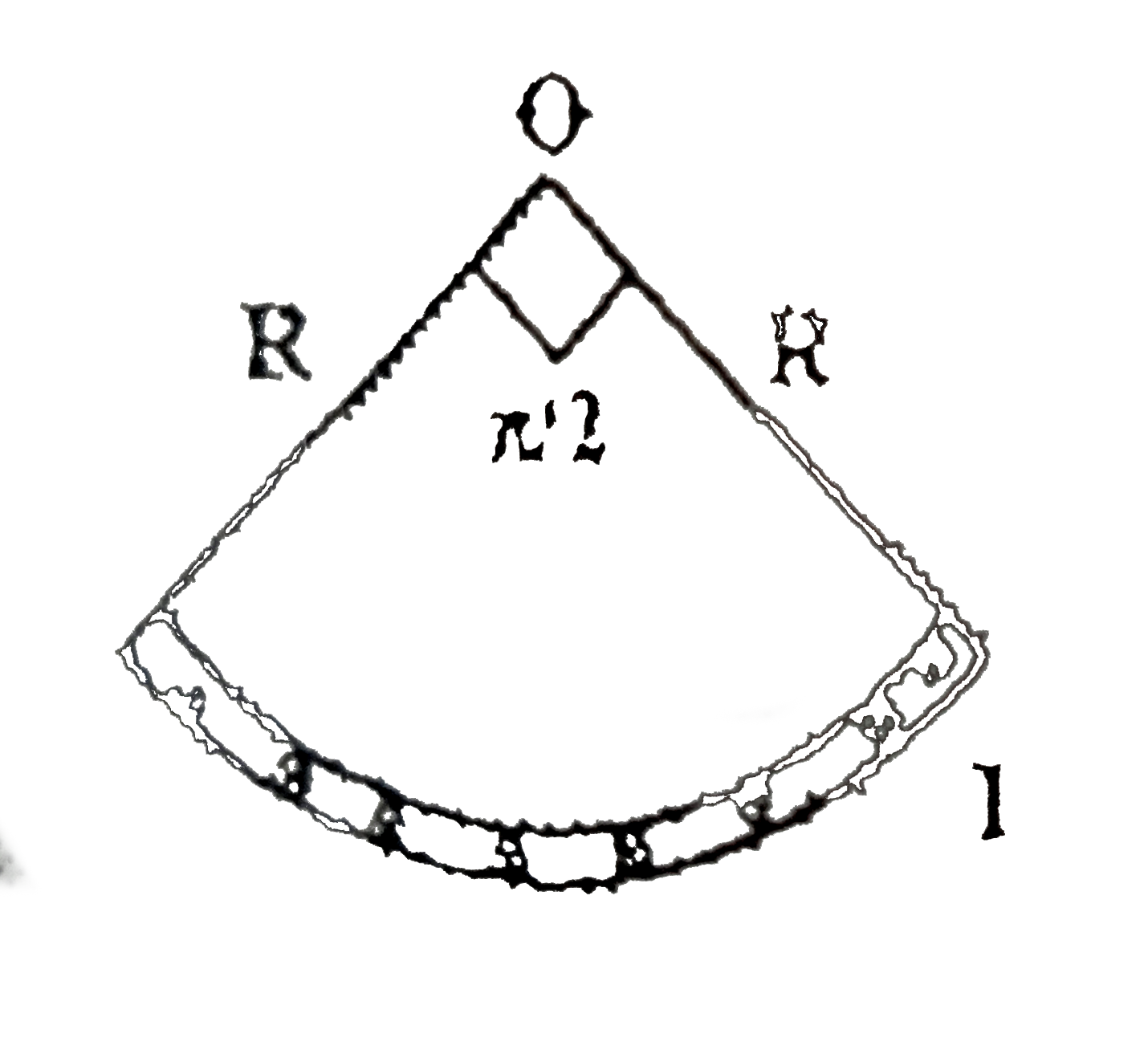 View Solution
View SolutionA current I flows along a straight conductor with round cross-section. Find the flux of the Poynting vector across the lateral surface of the conductor's segment with resistance R.
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
View SolutionA steady current is flowing in a conductor of non-uniform cross-section. The charge passing through any cross section per unit time is
View Solution1A current flows through an infinitely long straight wire. The magnetic field produced at a point 1 metres away from it is
View Solution

