A uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
magnetic field increases linearly from centre to surface
magnetic field decays inversely with distance r from the centre of wire for r>R
magnetic field at the centre of wire is zero
None of the above
Use Amperes Law
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Comprehension
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A long wire in the shape of a cylindrical shell of inner and outer radii R2 and R respectively carries a steady current I in a direction parallel to its length. This current is uniformly distributed across the area of cross-section of the wire. The magnetic field intensity at a point at a distance 3R4 from the axis of the wire is m(μ0IπR).. The value of m is _________.
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View Solution
Knowledge Check
A long cylindrical wire carries a steady current which is uniformly distributed across its cross section. Which of the following is true?
AMagnetic field is zero at the centre.BElectric field is zero at the centre.CElectric field just outside the cylinder is zero.DMagnetic field just outside the cylinder is zero.A cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
Aμ0I2π(R−x)Bμ0I2πxCμ0I2π(R+x)Dnone of theseA long straight wire of radius R carries a steady current which is uniformly distributed through the cross-section of the wire. The magnitudes of the magnetic field at distance r1 and r2 from the centre of the wire are B1 and B2 respectively. Then
AB1B2=r1r2,ifr1<R and r2<RBB1B2=r1r2,ifr1>R and r2>RCB1B2=r2r1,ifr1<R and r2<RDnone of these
A long straight conducting solid cylindrical wire of radius R carries a steady current / that is uniformly distributed throughout the cross section of the wire. Choose the correct graph of magnetic field B versus r (where r is distance from the axis of the wire)
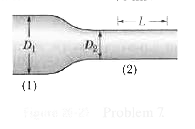
View SolutionFigure 26-21 shows wire section 1 of diameter D1=4.00R and wire section 2 of diameter D2=1.75R, connected by a tapered section. The wire is Copper and carries a current. Assume that the current is uniformly distributed across any cross-sectional area through the wire's width. The electric potential change V along the length L= 2.00 m shown in section 2 is 10.0μV. The number of charge carners per unit volume is 8.49×1028m−3. What is the drift speed of the conduction electrons in section 1?
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View Solution
