A current I flows an infinitely long wire with cross section in the form of a semi - circular ring of radius R. The magnitude of the magnetic induction along its axis is :
μ0I2π2R
μ0I2πR
μ0I4π2R
μ0Iπ2R
The correct Answer is:D
Consider two elements on semicircular cross-section of long wire at C and D, each of length dl symmetrically situated with respect to point O cross-section as shown in figure. Current through each element,
dI=Iπrdl and dl=rdθ,
∴dI=Iπrrdθ=Iπdθ
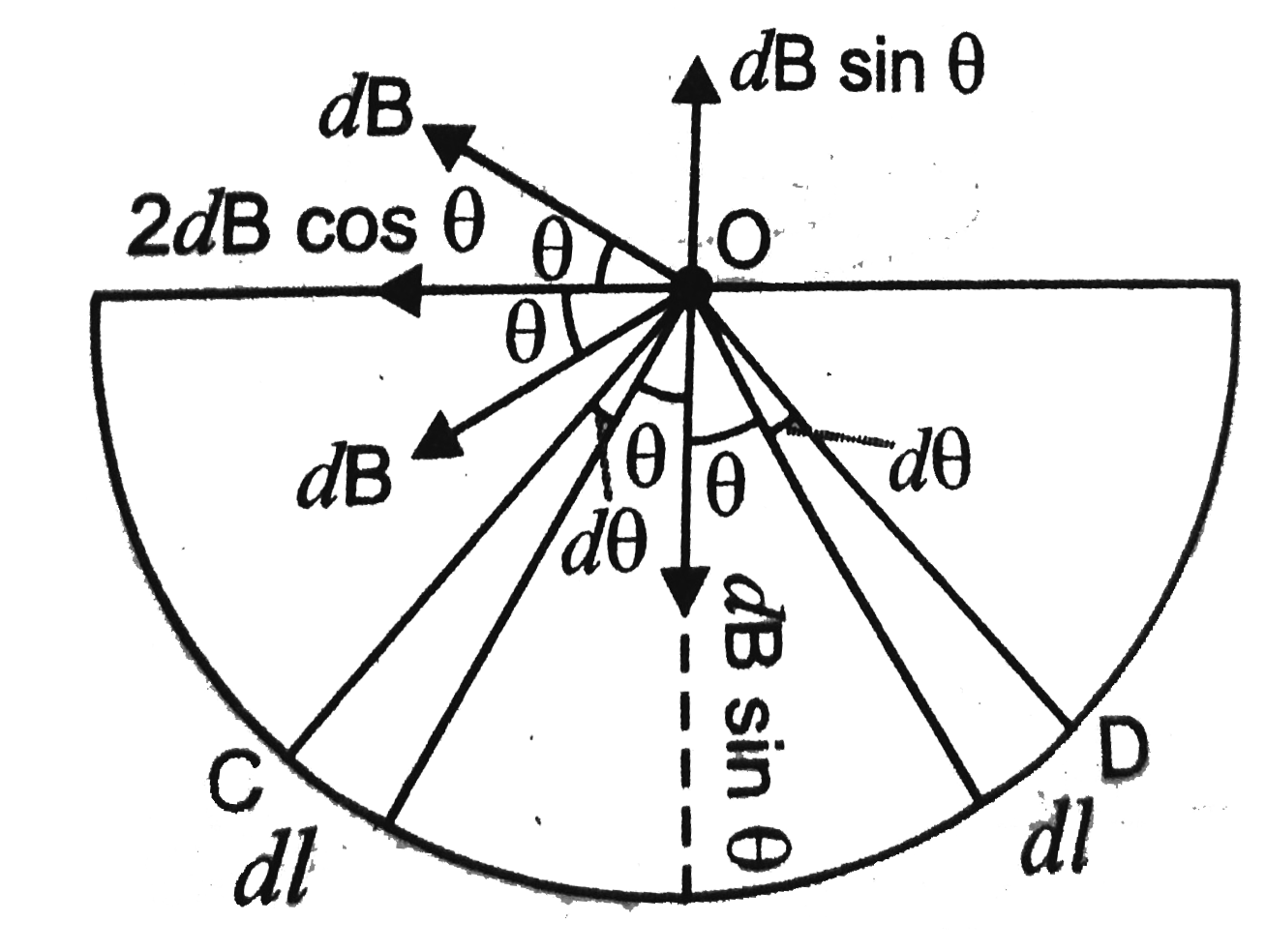
Magnitude of magnetic field induction at O due to current dI in element at C or D is
dB=μ04π2dIr=μ0dI2πr
Net magnetic field induction at O due to both the elements carrying current dI is
=2(dB)cosθ=2×μ02πdIrcosθ
=μ0πr×(Iπdθ)cosθ=μ0Iπ2rcosθdθ
Total magnetic field induction at O due to current through the entire wire is
B=μ0Iπ2r∫π/20cosθdθ=μ0Iπ2r[sinπ2−sin0]=μ0Iπ2r
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (a)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (c)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Value Based Questions
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A current I flows in a long straight wire whose cross section is in the shape of a thin quarter ring of radius R. Find the induction of the magnetic field (B) at point O on the axis.

View SolutionA current I flows in a long straight wire with cross-section haviing the form of a thin half-ring of radius R (Fig). Find the induction of the magnitude field at the point O.

View Solution
Knowledge Check
A long straight wire is placed along the axis of a circuit ring of radius R. The mutual inductance of this system is
Aμ0R2Bμ0πR2Cμ02D0A wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is
 Aμ02r(π−θ+tanθ)Bμ0I2πR(π+θ−tanθ)Cμ0I2πR(π−θ+tanθ)Dμ0I2πR(−tanθ+π−θ)
Aμ02r(π−θ+tanθ)Bμ0I2πR(π+θ−tanθ)Cμ0I2πR(π−θ+tanθ)Dμ0I2πR(−tanθ+π−θ)A current I=IA flowing through an infinite long wire A1 divides between two infinite long wires A2 and A3 at junction B. The magnitude of the magnetic field at point O due to current through wires is :
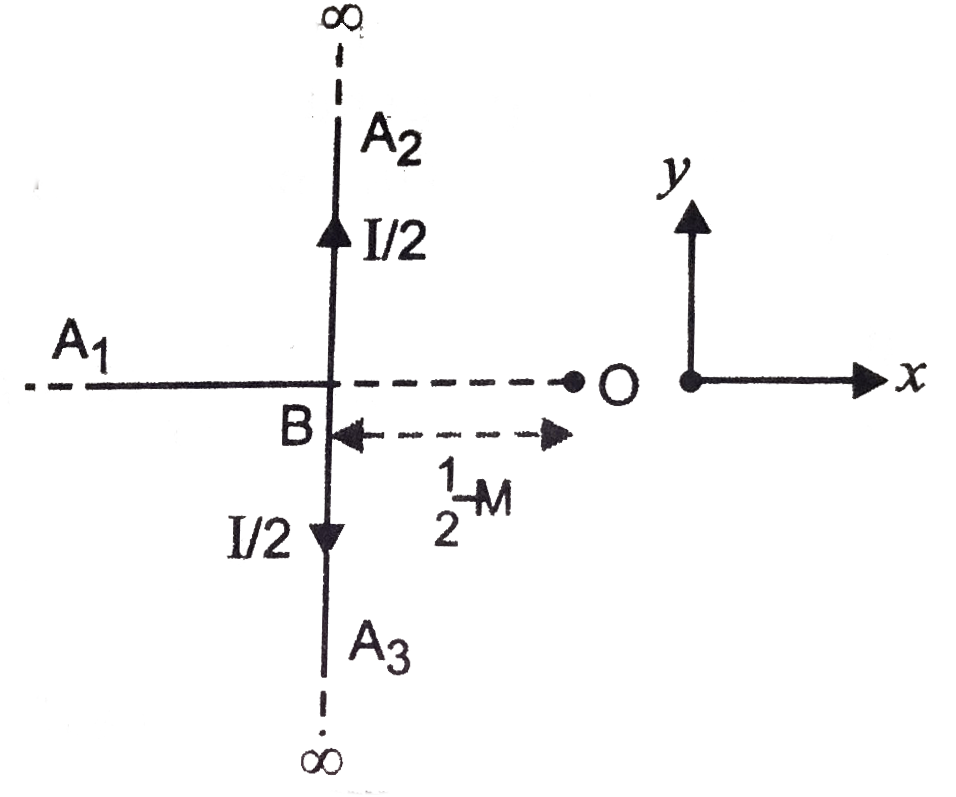 AzeroB2×10−7TC4×10−7TD8×10−7T
AzeroB2×10−7TC4×10−7TD8×10−7T
A direct current I flows in a long straight conductor whose cross section has the form of a thin halr-ring of radius R. The same current flows in the opposite direction along a thin conductor located on the axis of the first conductor. Find the magnetic induction froce between the given conductors reduced to a unit of their length.

View SolutionA current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
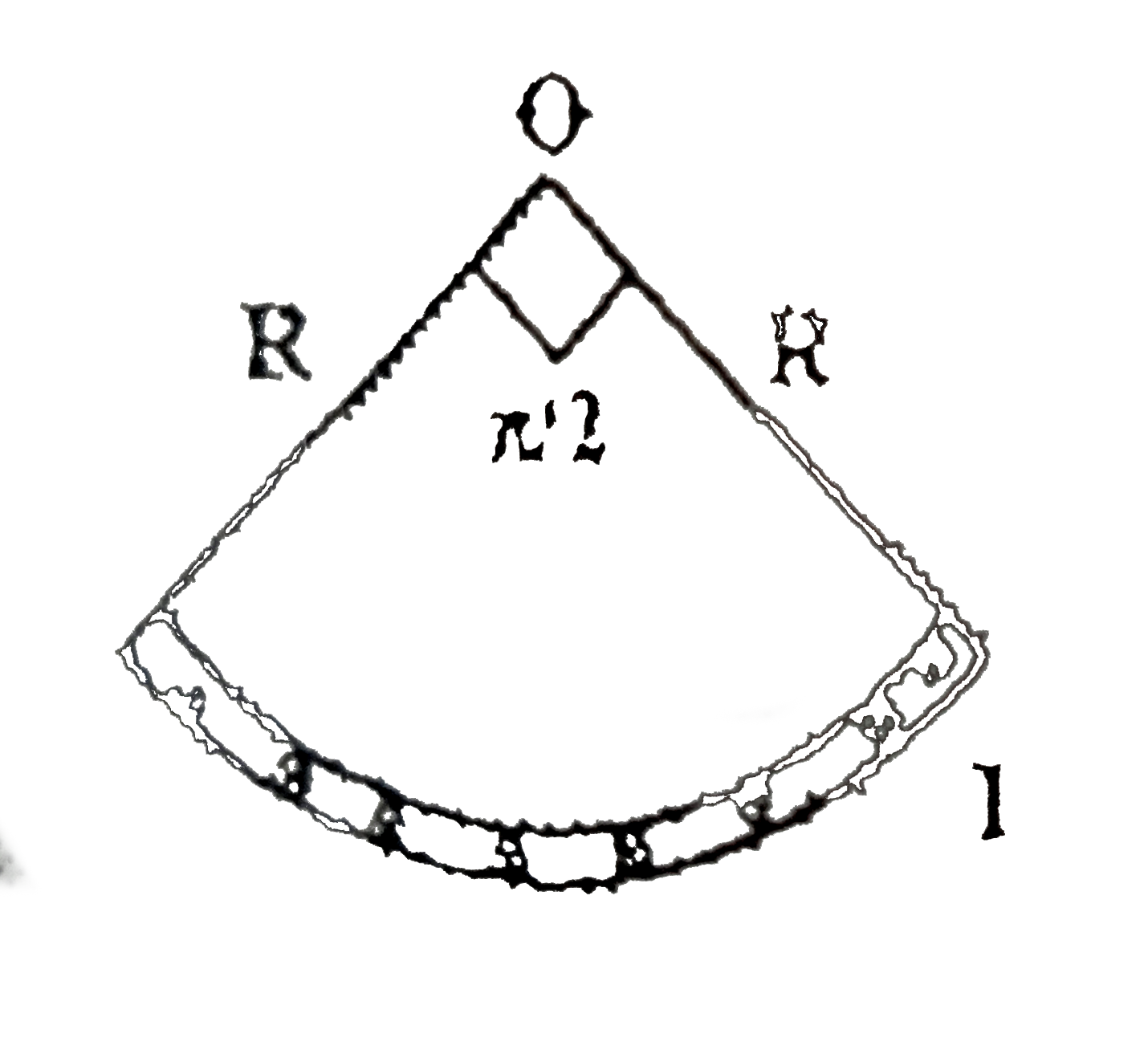
View SolutionA steady current I flows along an infinitely long straight wire with circular cross-section of radius R. What will be the magnetic field outside and inside the wire at a point r distance far from the axis of wire?
View SolutionA thin wire is bent in the form of a semi circular ring of radius R=0.9m carries a current I=1amp . The magnetic induction at a point P as shown in the fig. is given by nX10−7 Tesla. Find the value of n.[ln(√2+1)=0.9]

View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View Solution
