A charge $Q$ is uniformly distributed over the surface of non - conducting disc of radius $R$ . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:

A

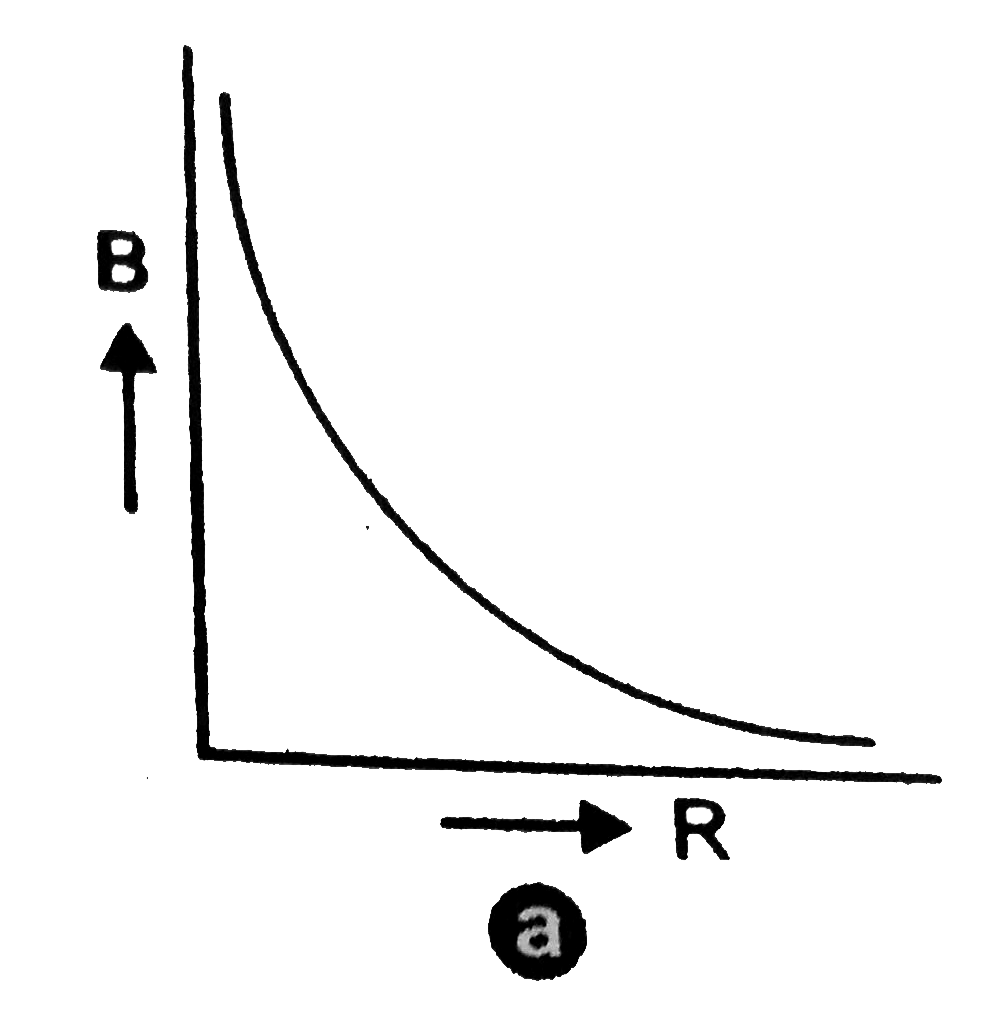
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Face area of disc $= π R^{2}$
Charge per unit area of disc $= \frac{Q}{π R^{2}}$
Consider an elementary ring of disc of radius r and thickness dr, as shown in figure. Face area of elementary ring $= 2 π r d r$
Change on elementary ring,
$d q = \frac{Q}{π R^{2}} \times 2 π r d r = \frac{2 Q r d r}{R^{2}}$

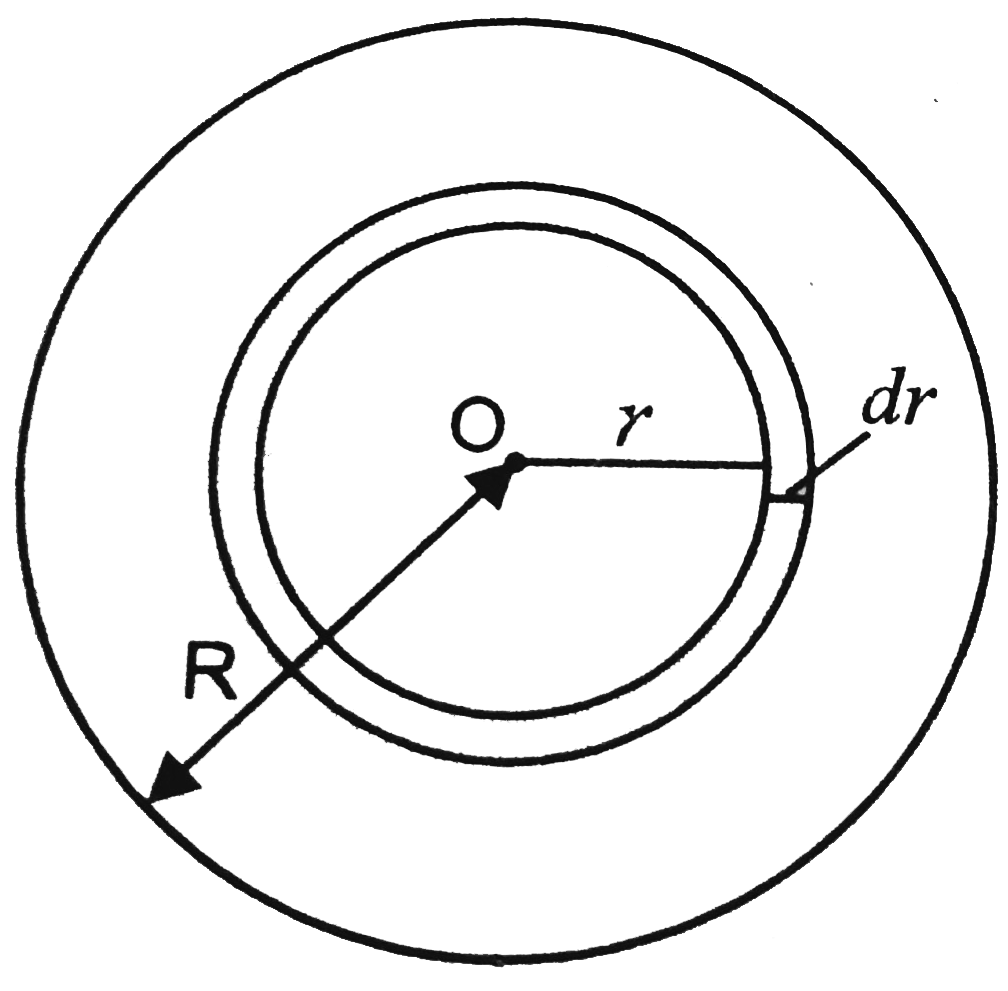
Time period of rotation of disc, $T = 2 \frac{π}{ω}$
Current I associated with rotating charge $d q$ is
$I = \frac{d q}{T} = \frac{2 Q r d r / R^{2}}{2 π / ω} = \frac{Q ω d r}{π R^{2}}$
Magnetic field induction $d B$ at the centre O of the elementary ring due to current I is
$d B = \frac{μ_{0}}{4 π} \frac{2 π I}{r} = \frac{μ_{0} I}{2 r} = \frac{μ_{0}}{2 r} \times \frac{Q ω r d r}{π R^{2}} = \frac{μ_{0} Q ω d r}{π R^{2}} = \frac{μ_{0} Q ω d r}{2 π R^{2}}$
Total magnetic field induction at O due to entire rotating disc is
$B = \int_{0}^{R} \frac{μ_{0} Q ω d r}{2 π R^{2}} = \frac{μ_{0} Q ω R}{2 π R^{2}} = \frac{μ_{0} Q ω}{2 π R}$
$∴ B \propto \frac{1}{R} (∵ Q$ and $ω$ are unchanges)
Hence, variation of B and R should be a rectangular hyperbola as re[resenmted in option (a).

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
A $\frac{R}{2}$
B $\frac{R}{\sqrt{2}}$
C $\frac{R}{\sqrt{3}}$
D $\frac{R}{3}$
Question 2 - Select One
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
A $R / \sqrt{2}$
BR/2
C $\sqrt{2}$ R
D2R
Question 3 - Select One
Circular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
A8
B4
C2
D1

PRADEEP-MAGNETIC EFFECT OF CURRENT AND MAGNETISM-Exercise

Home
Ask Doubt
Profile