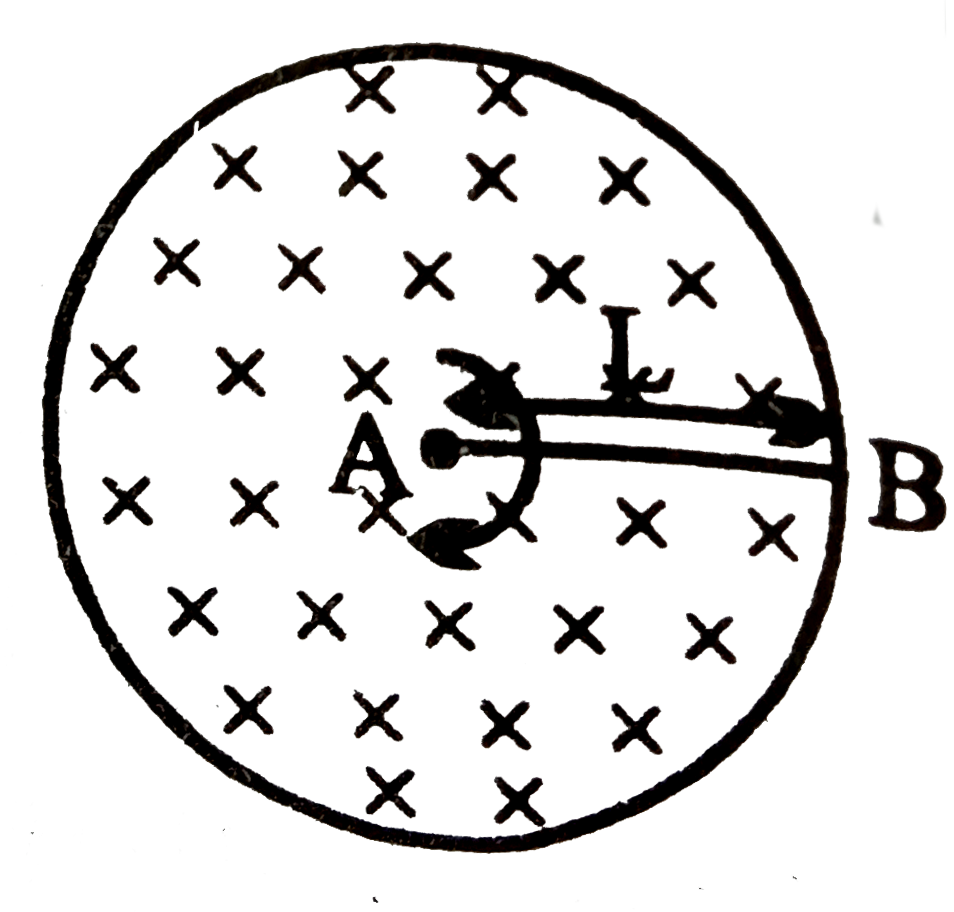
Calculate the rate at which the flux linked with the generated area changes with time when a rod length l is (a) translated (b) rotated in a uniform field of induction B as shown in fig.
(a) Component of velocity perpendicular to the rod =υsinθ. Therefore, in time t, area traversed =l×υsinθ×t.
∴ϕ=B(lxυsinθ×t)cos0∘=Blυtsinθ
dϕdt=Blυsinθ
(b) In time t, if θ is the angle traced by the free end, then
∴ Area swept, A=πl2×(θ2π)=12l2θ
ϕ=B(12l2θ)cos0∘=12B,l2θ
dϕdt=12Bl2dθdt=12Bl2ω
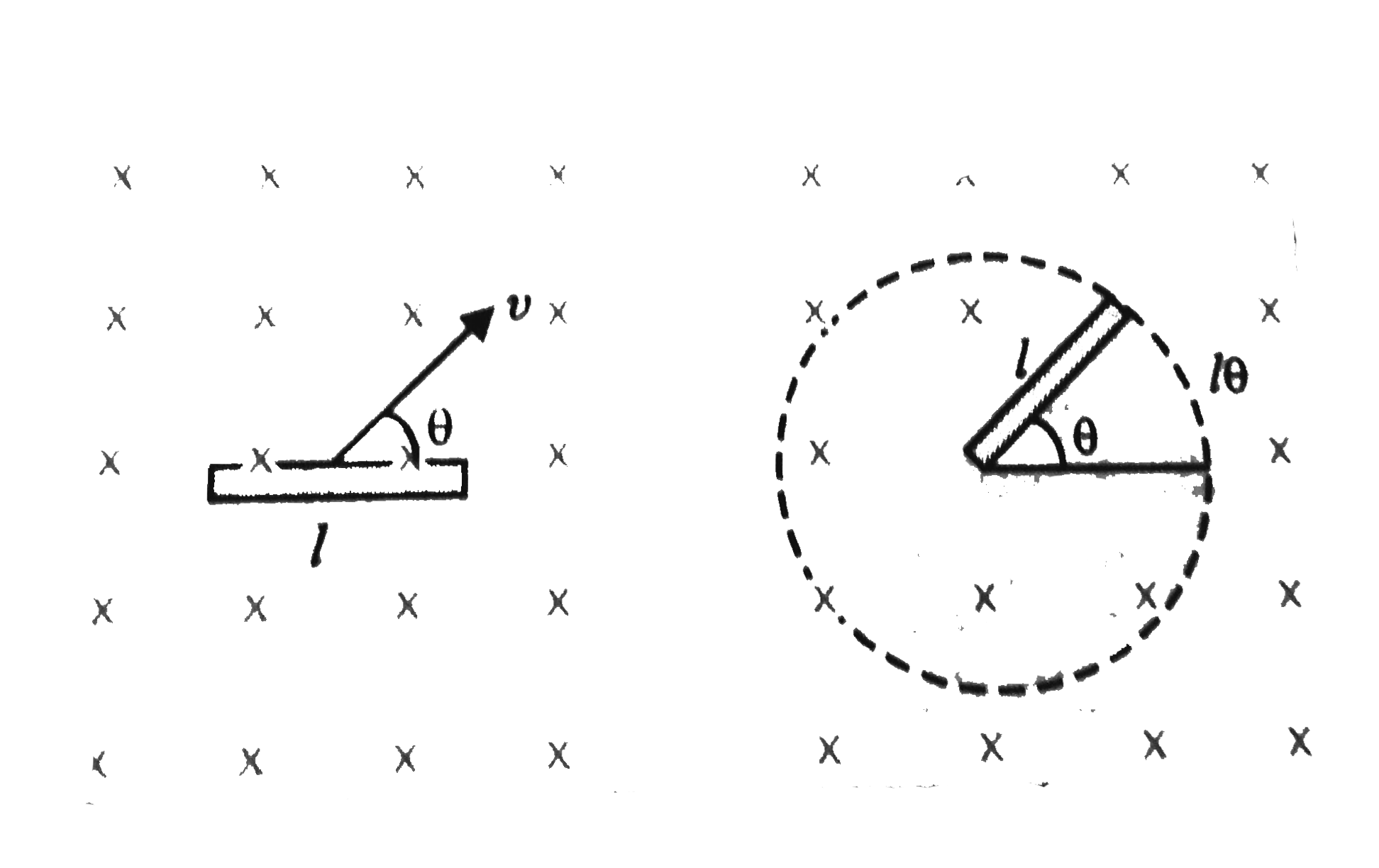
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
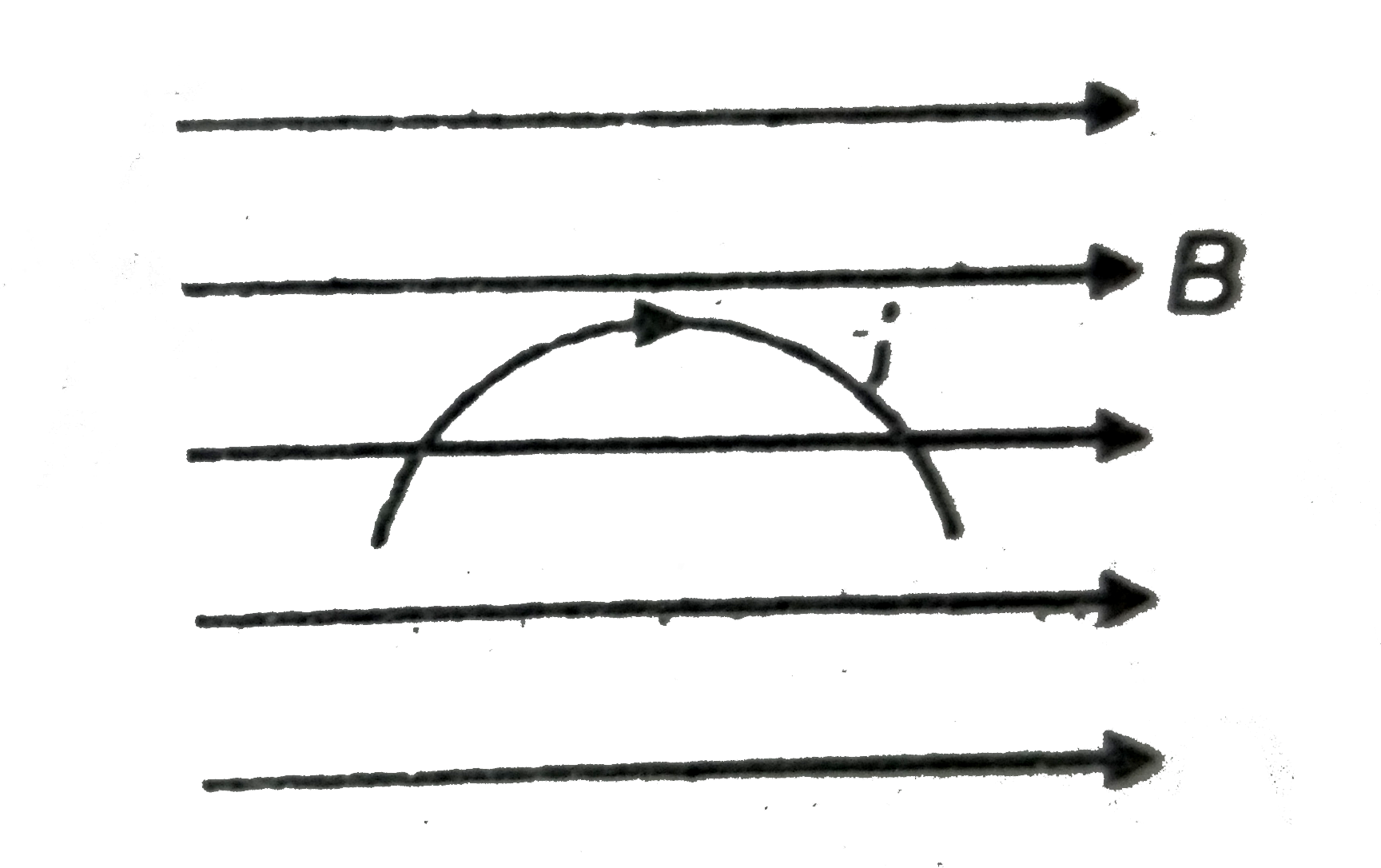
What is the force experienced by a semicircular wire of radius R when it is carrying a current l and is placed in a uniform magnetic field of induction B as shown in figure. ?
 View Solution
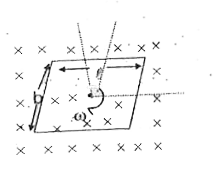
View SolutionA rectangular loop of length l and breadth b is situated in a uniform magnetic field of induction B with its plane perpendicular to the field as shown in the figure . Calculate the rate of change of magnetic flux and the induced emf if the loop is rotated with constant angular velocity ω
(a) about an axis passing through the centre and perpendicular to the loop.
(b) about an axis passing through the centre parallel to the breadth through angle 180∘ .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __
 AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating
AThen the end X of the rod becomes positively chargedBThe end Y of the rod becomes positively chargedCThe entire rod is unevenly chargedDThe rod becomes hot due to joule heating - Question 2 - Select One
Rate of charges of torque τ with deflection theta is maximum for a magnet susended freely in a uniform magnetic field of induction B, when
Aθ=0∘Bθ=45∘Cθ=60∘Dθ=90∘ - Question 3 - Select One
The rate of change of torque 'τ' with deflection θ is maximum for a magnet suspended freely in a uniform magnetic field of induction B when θ is equal to
A0∘B45∘C60∘D90∘
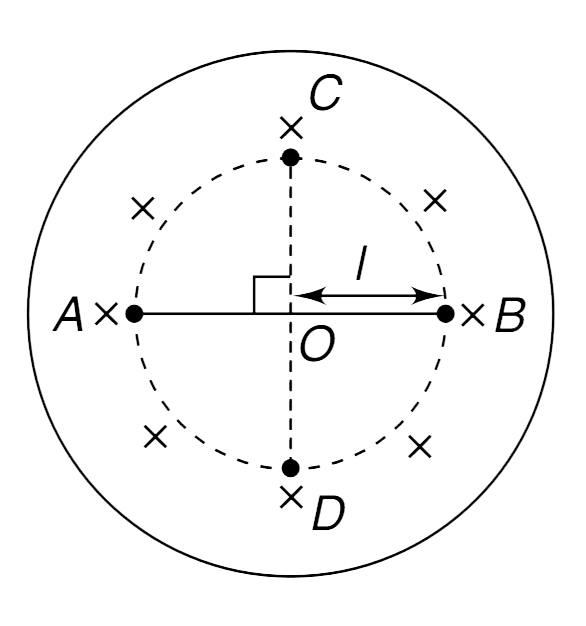
A massless non conducting rod AB of length 2l is placed in uniform time varying magnetic field confined in a cylindrical region of radius (R>l) as shown in the figure. The center of the rod coincides with the centre of the cylin- drical region. The rod can freely rotate in the plane of the Figure about an axis coinciding with the axis of the cylinder. Two particles, each of mass m and charge q are attached to the ends A and B of the rod. The time varying magnetic field in this cylindrical region is given by B=B0[1−t2] where B0 is a constant. The field is switched on at time t=0. Consider B0=100T,l=4cmqm=4π100C/kg. Calculate the time in which the rod will reach position CD shown in the figure for th first time. Will end A be at C or D at this instant ?
 View Solution
View SolutionThe magnetic flux linked with a vector area →A in a uniform magnetic field →B is
View SolutionA hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
View SolutionWhen a rod of length l is rotated with angular velocity of ω in a perpendicular field of induction B , about one end , the emf across its ends is
View SolutionA copper rod AB of length L, pivoted at one end A, rotates at constant angular velocity omega, at right angles to a uniform magnetic field of induction B. The e.m.f developed between the mid point C of the rod and B is
 View Solution
View Solution

