Doubtnut Promotions Sticky

Consider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula ϕ=B1.dA1+B2.Da2+……..Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.
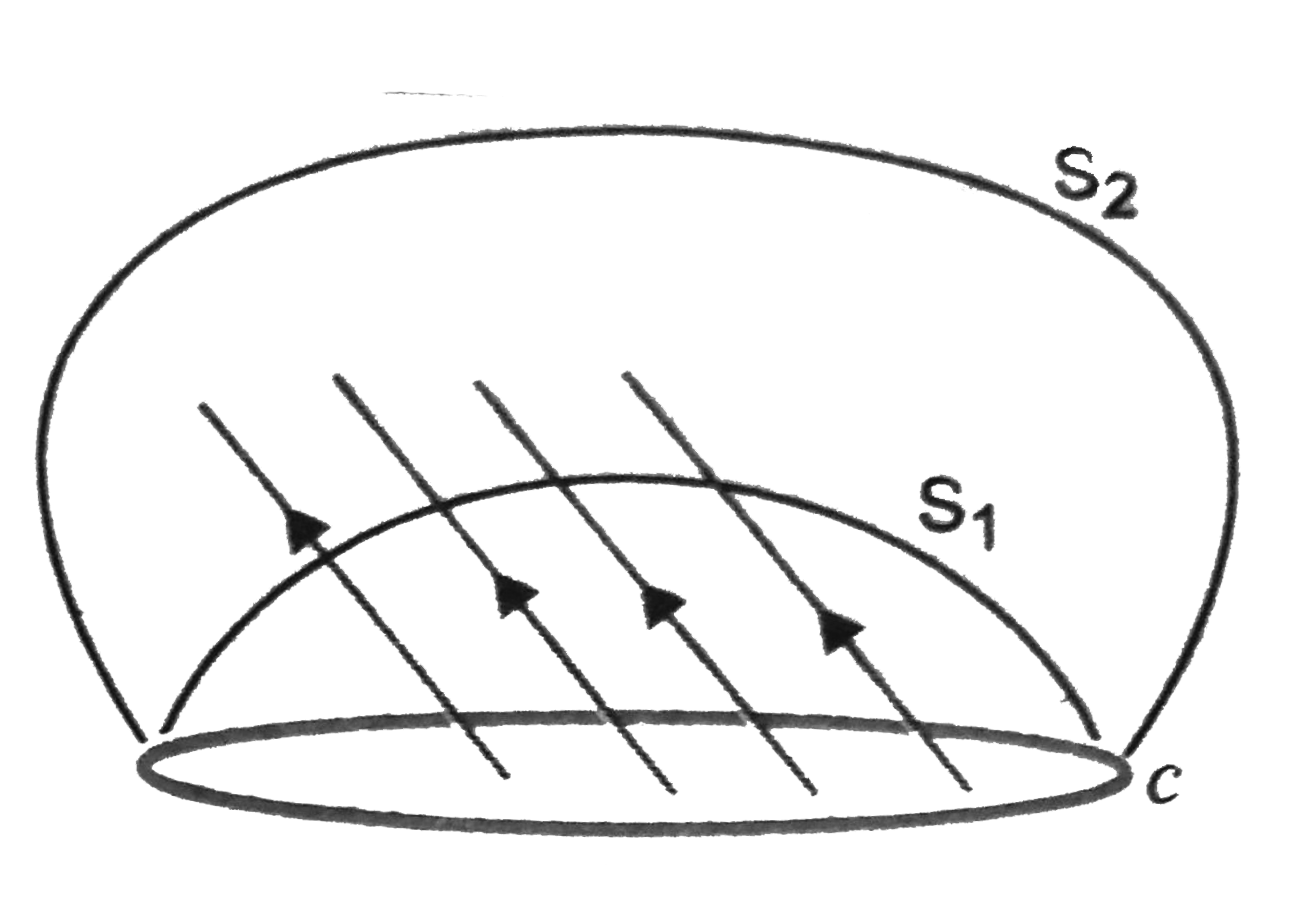
Consider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula phi = B(1) .dA(1) + B(2). Da(2) +……..Now if we chose two different surfaces S(1) and S(2) having C as their edge, would we get the same answer for flux. Justify your answer.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We would get the same answer for magnetic flux. This is because magnetic flux = number of magnetic field lines passing through the surface (dϕ=→B.Δ→S). As magnetic field lines form closed continuos loops and cannot end or start in space, therefore in Fig. number of magnetic lines passing through surface S1 must be the same as the number of magnetic lines through the surface S2.

|
Updated on:21/07/2023
Class 12PHYSICSELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The magnetic flux across a loop of resistance 10Ω is given by ϕ=(5t2−4t2+1)Wb. How much current is induced in the loop after 0.2 s?

    A0.4 A
    B0.2 A
    C0.04 A
    D0.02 A
  • Question 2 - Select One

    A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
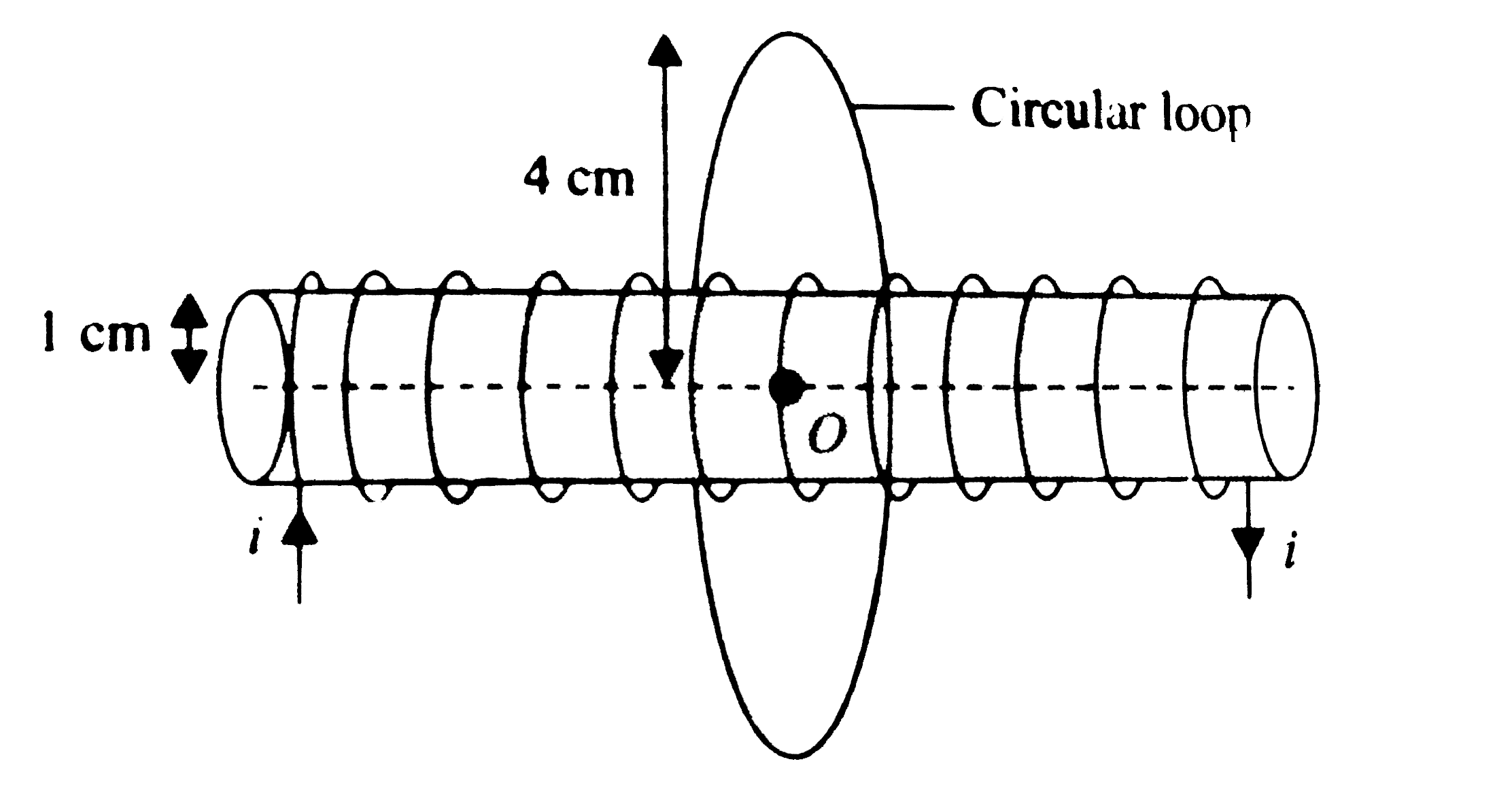
    ocr_image
    A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
    Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.

    A4.7×10−7Vm−1
    B3.82×10−6Vm−1
    C2.3×10−5Vm−1
    DNone of these
  • Question 3 - Select One

    A square non - conducting loop , 20 cm , on a side is placed in a magnetic field . The centre of side AB coincides with the centre of magnetic field . The magnetic field is increasing at the rate 2 T /s . The potential difference betweeen B and C is :
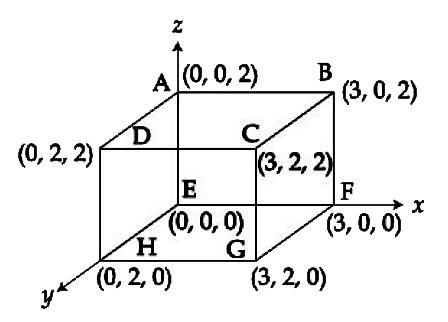
    ocr_image

    A30 m V
    Bzero
    C10 mV
    D20 m V