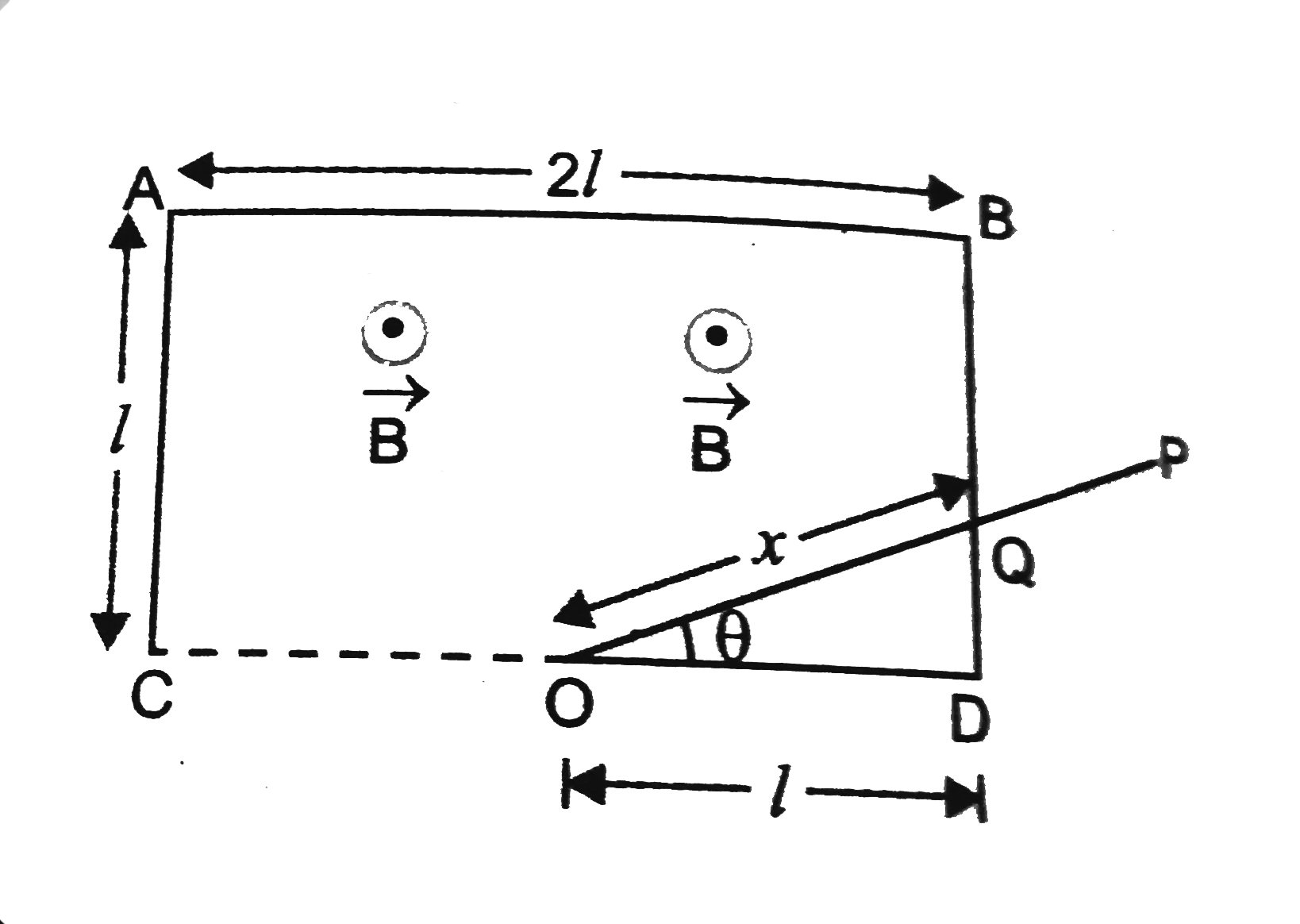
ODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity $ω$ (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of $λ$ per unit length. Find the current in the rotating conductor, as it rotates by $180^{\circ}$ .

Video Solution

Text Solution

Verified by Experts

The set up is shon in Fig Between time
t = 0 $t = \frac{T}{8} = \frac{π}{4 ω}$ , the rod OP will make contach
with side BD. At any time t: $0 < t < \frac{π}{4 ω}$ , let the length
$∴$ Magnetic flux through the area ODQ is
$ϕ = B \times a r e a O Q D = B \times \frac{1}{2} Q D \times O D = B \times \frac{1}{2} l \tan θ \times l$

$ϕ = \frac{1}{2} B l^{2} \tan θ$ , where $θ = ω t$
Magnetic of emf generated, $e = \frac{d ϕ}{d t} = \frac{1}{2} B l^{2} ω \sec^{2} ω t$
If R is resistance of the rod in contact, then induced current $I = \frac{e}{R}$ .
Now , $R = λ x = \frac{λ l}{\cos ω t} ∴ I = \frac{1}{2} \frac{B l^{2} ω \sec^{2} ω t}{λ l / \cos ω t} = \frac{B l ω}{2 λ \cos ω t}$
For $t = \frac{T}{8} = \frac{π}{4 ω}$ to $t = \frac{3 T}{8} = \frac{3 π}{8}$ , the rod is contact with
the side AB, as shown in Fig. Let the length of the rod in contant, OQ = x.
Magnetic flux linked with area ODBQ
$ϕ = B \times$ area of trapezium ODBQ $= B (l^{2} - \frac{l^{2}}{2 \tan θ})$ , where $θ = ω t$

Magnitude of emf generated, $e = \frac{d ϕ}{d t} = \frac{1}{2} B l^{2} ω \sec^{2} ω t = \frac{1}{2} B l^{2} ω \frac{\sec^{2} ω t}{\tan^{2} ω t}$
Induced current, $I = \frac{e}{R} = \frac{e}{λ x} = \frac{e \sin ω t}{λ l} = \frac{1}{2 λ} \times \frac{B l ω}{\sin ω t}$
For $t = \frac{3 T}{8} = \frac{3 π}{4 ω}$ to $t = \frac{4 T}{8} = \frac{π}{ω}$ , the rod is in contact with
the side AC as shown in Fig.
Let the length of the rod in contact OQ = x.
Magnetic flux linked with area ODBAQ
$ϕ = B \times$ [area of rectangular ABDC - area of $Δ O Q C$ ]

$ϕ = B [2 l^{2} - \frac{l^{2}}{2 \tan ω t}]$
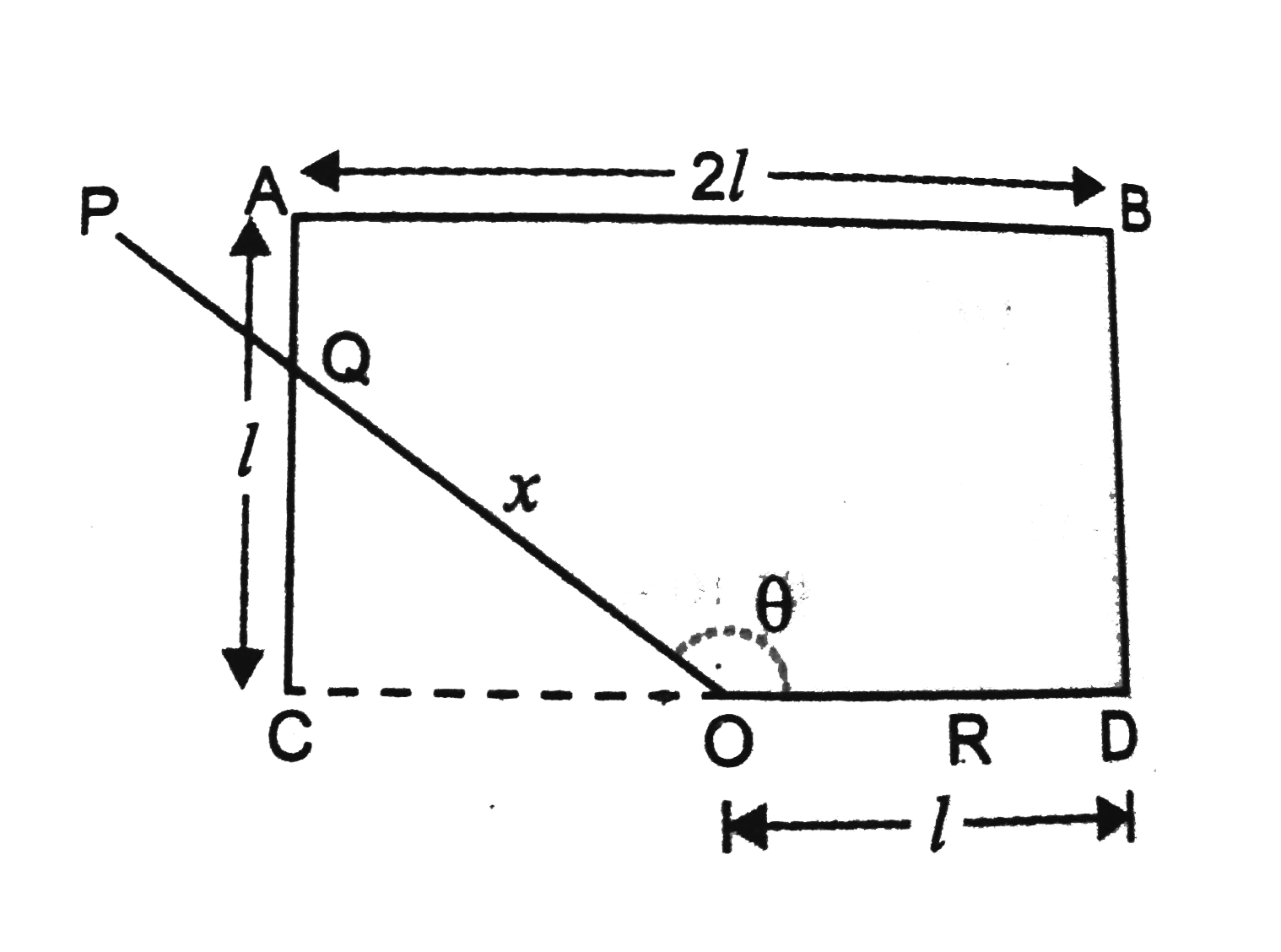
Magnitude of induced emf, $e = \frac{d ϕ}{d t} = \frac{d}{d t} B (2 l^{2} - \frac{l^{2}}{2 \tan ω t}) = \frac{B ω l^{2} \sec^{2} ω t}{2 \tan^{2} ω t}$
Induced current, $I = \frac{e}{R} = \frac{e}{λ x} = \frac{e \sin ω t}{λ l} = \frac{B l ω}{2 λ \sin ω t}$

Updated on:21/07/2023

The electrical resistance of a conductor
Avaries directly proportional to its area of cross-section.
Bdecreases with increase in its temperature.
Cdecreases with increase in its conductivity.
Dis independent of its shape but depends only on its volume.
The resistance of a conductor depends on its
ALength
Barea of cross section
Ctemperature
Dall of these
A circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is $4 ω$ . The net magnetic field at the centre of the conductor is

A $\frac{μ_{0}}{2}$
B $\frac{8 μ_{0}}{3}$
C $2 μ_{0}$
Dzero