Consider the LCR circuit shown in Fig. Find the net current I and the phase of i. show that i=υZ . Find the impedence Z for this circuit.
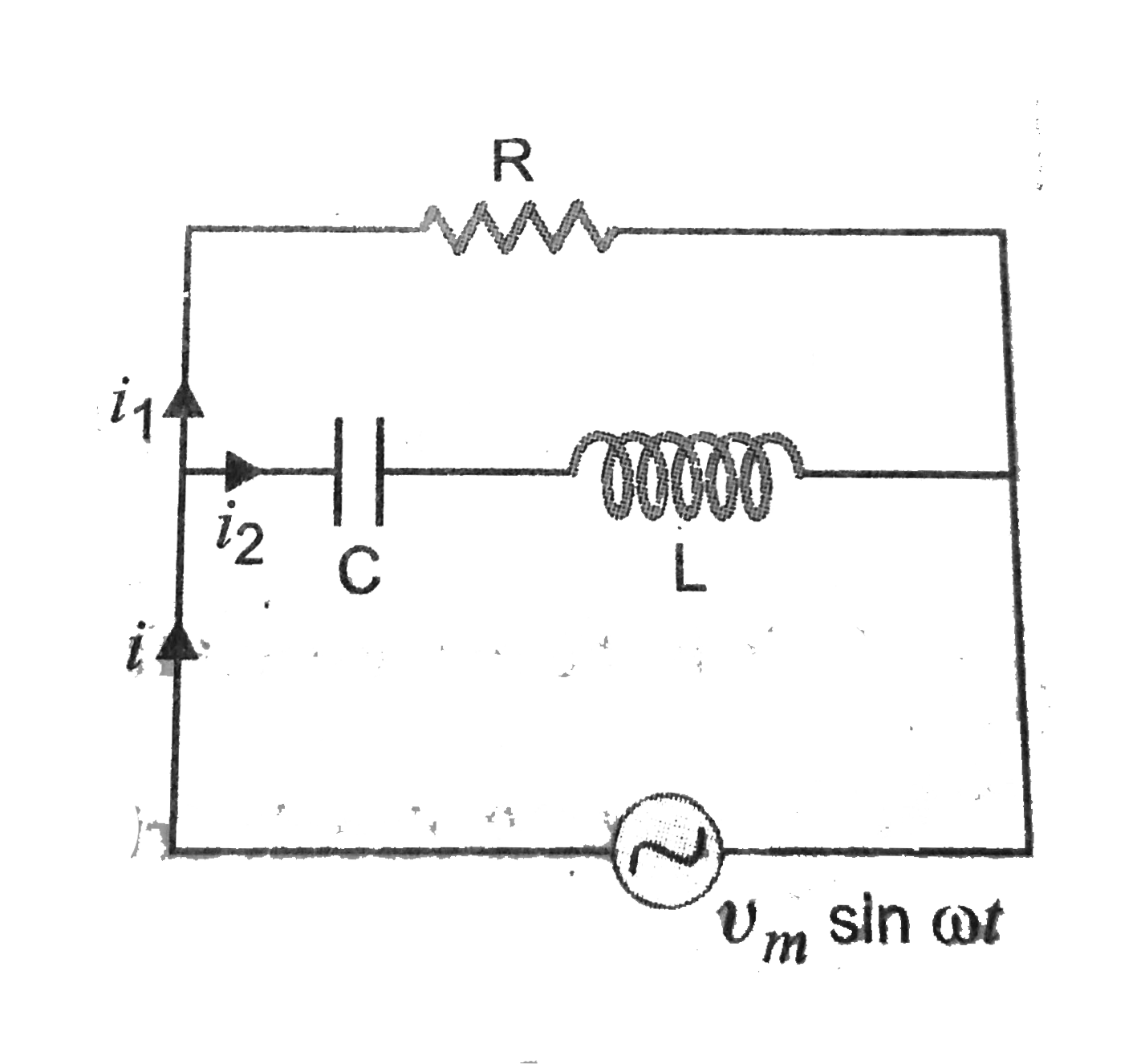
Text Solution
In Fig. let i. be the total current form the source. It is divided into two parts : i1 through R and i2 through series combination of C and L, such that i=i1+i2.
As Ri1=υmsinωt,i1=υmsinωtR
If q2 is charge on C at time t, then for series combination of C and L,
q2C+dq22dt2=υmωt
Let q2=qmsin(ωt+ϕ)
∴dq2dt=qmωcos(ωt+ϕ) and d2q2dt=−qmω2sin(ωt+ϕ)
Putting in (ii), we get qm[1C=Lω2]sin(ωt+ϕ)−υmsinωt
If ϕ=0 and (1C−Lω2)>0, then qm=υm(1C−Lω2)
From (iii), i2=dq2dt=ωqmcos(ωt+ϕ) , using (iv), i2=ωυmcos(ωt+ϕ)1C−Lω2
Taking ϕ=0, i2=υmcos(ωt)(1ωC−Lω)
From (i) and (v), we find that i1 and i2 are out of phase.
Now, i1+i2=υmsinωtR+υmcosωt(1ωC−Lω)
Put υmR=A=Ccosϕ and υm(1ωC−Lω)=B=Csinϕ
∴i1+i2=Ccosϕsinomegt+Csinϕcosωt=Csin(ωt=ϕ)
Where C=√A2+B2 and ϕ=tan−1(BA)
C=⎡⎢
⎢
⎢⎣υ2mR2+υ2m(1ωC−Lω)2⎤⎥
⎥
⎥⎦1/2 and ϕ(tan−1)R(1ωC−Lω)
Hence, i=i1+i2=⎡⎢
⎢
⎢⎣υ2mR2+υ2m(1ωC−Lω)2⎤⎥
⎥
⎥⎦1/2sin(ωt+ϕ)
or iυm=1Z=⎡⎢
⎢
⎢⎣1R2=1(1ωC−Lω)2⎤⎥
⎥
⎥⎦1/2
This is the expression for impedance Z of the circuit.
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Very Short Answer Qusetions
1 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Value Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NCERT Question
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
Similar Questions
Consider the LCR circuit shown in Fig. Find the net current I and the phase of i. show that i=υZ . Find the impedence Z for this circuit.

View SolutionConsider the L-C-R circuit shown in the fiure. Find the net current I and the phase of i. Show that i=VZ. Find the impedance Z of this circuit.

View Solution
Knowledge Check
Find the current I in circuit
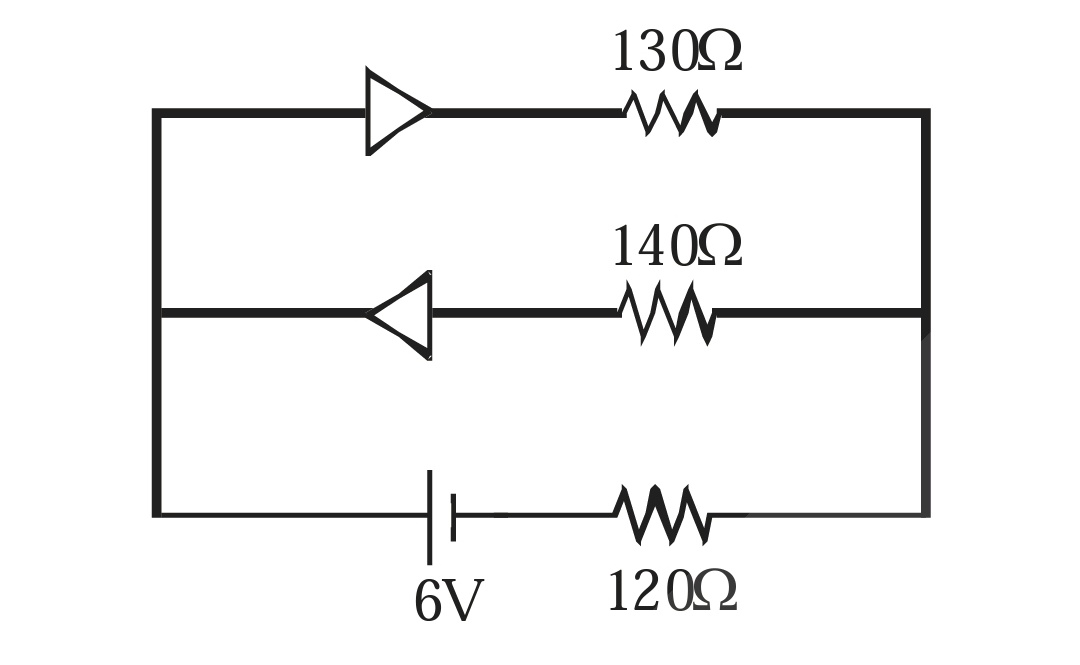 A20 mAB2 mAC0.1 mAD10 mA
A20 mAB2 mAC0.1 mAD10 mAConsider the circuit shown in the figure. The current I3 is equal to
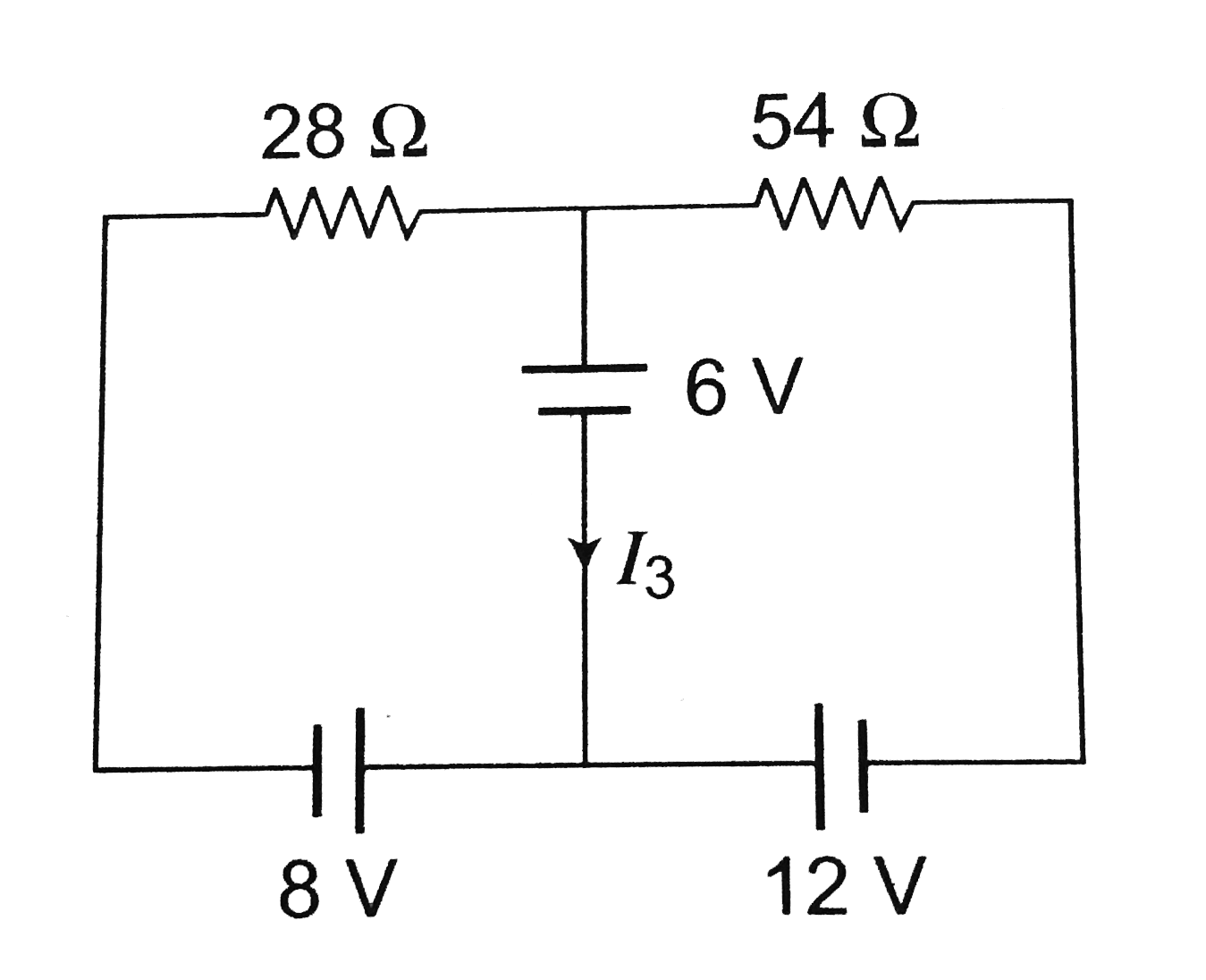 A5ampB3ampC−3ampD−5/6amp
A5ampB3ampC−3ampD−5/6ampFind the current I in the given circuit
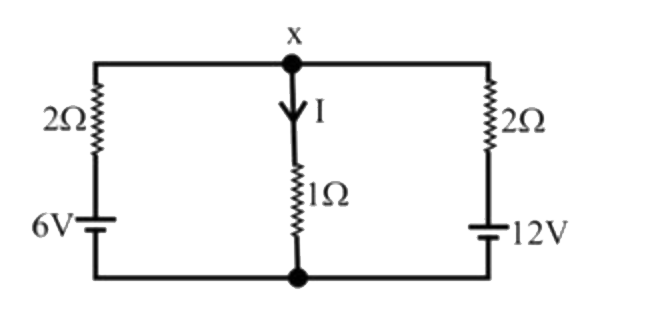 A2AB4. 5 AC6AD1.5 A
A2AB4. 5 AC6AD1.5 A
Consider the L-C-R circuit shown in the fiure. Find the net current I and the phase of i. Show that i=VZ. Find the impedance Z of this circuit.

View SolutionConsider the circuit shown in the figure. The current I3 is equal to

View SolutionFind the current I in the given circuit

View SolutionConsider the circuit shwon in fig. The circuit is in steady state.

The value of i1 is
View SolutionConsider the circuit shown in the figure. The current i3 is equal to
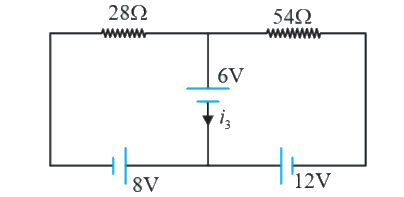
View Solution
