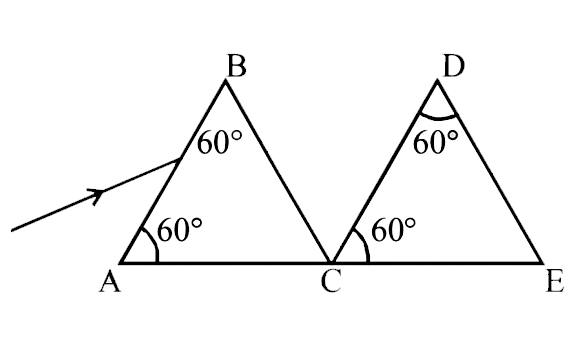
A ray of light is incident on a prism $A B C$ of $μ = \sqrt{3}$ as shown in Fig. Find the angle of incidence for which the deviation of light by the prism $A B C$ is minimum.
By what angle should the second prism be rotated so that final ray suffers net minimum deviation ?

Video Solution

Text Solution

Verified by Experts

Let $i_{1}$ be the angle of incidence of ray on face $A B$ of the first prism and $r_{1}$ corresponding angle of refraction on face $A B$ . If $r_{2}$ is angle of incidence on the face $B C$ of the prism, then in the minimum deviation position,
$r_{1} = r_{2} = A / 2 = 60^{\circ} / 2 = 30^{\circ}$
According to Snell's Law
$μ = \frac{{sin i}_{1}}{{sin r}_{1}}$
${sin i}_{1} = μ {sin r}_{1} = \sqrt{3} {sin 30}^{\circ} = \frac{\sqrt{3}}{2}$
$∴ i_{1} = 60^{\circ}$
For the final ray from the combination of prism to suffer net minimum deviation, the second prism $C D E$ must be rotated anticlockwise through $60^{\circ}$ so that opposite faces of the combination become parallel.

Updated on:21/07/2023

A ray of light is incident on a prism as shown in fig. Find the total deviation suffered by the ray if $∠ B A C = 1^{\circ}$ and $∠ C A D = 2^{\circ}$ .

A $1^{\circ}$
B ${1.5}^{\circ}$
C ${2.5}^{\circ}$
D $2^{\circ}$
A ray of light is incident on a $60^{\circ}$ prism at the minimum deviation position. The angle of refraction at the first face (i.e. incident face) of the prism is-
Azero
B $30^{\circ}$
C $45^{\circ}$
D $60^{\circ}$
A ray of light is incident on a $60^{\circ}$ prism at the minimum deviation position. The angle of refraction at the first face (i.e. incident face) of the prism is-
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
DZero