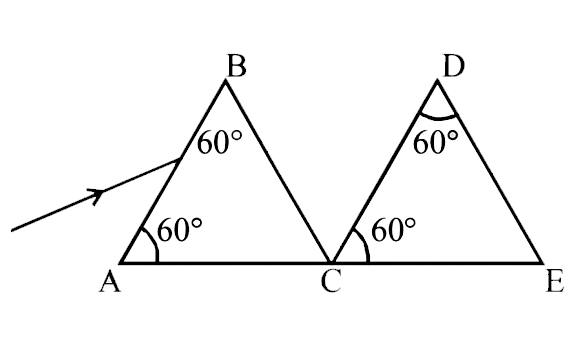
Two identical prism of index √3 are kept as shown in the figure. A light ray strikes the first prism at face AB. Find,
(a) the angle of incidence, so that the emergent ray from the first prism has minimum deviation.
(b) through what angle the prism DCE should be rotated about C so that the final emergent ray also has minimum deviation.
The correct Answer is:A, B, C

(a) For minimum deviation of emergent ray from the first prism. MN is parallel to AC
∵∠BMN=60∘
∵ ∠r=30∘
Applying Snell's law at M
μ=sinisinr
sini=μsinr
sini=√3×sin30∘=√32 ⇒i=60∘
(b) When the prism DCE is rotated about C in anticlockwise direction by 60∘, as shown in the figure, then the final emergent ray SR becomes parallel to the incident ray TM. Thus, the angle of deviation becomes zero.

Topper's Solved these Questions
Similar Questions
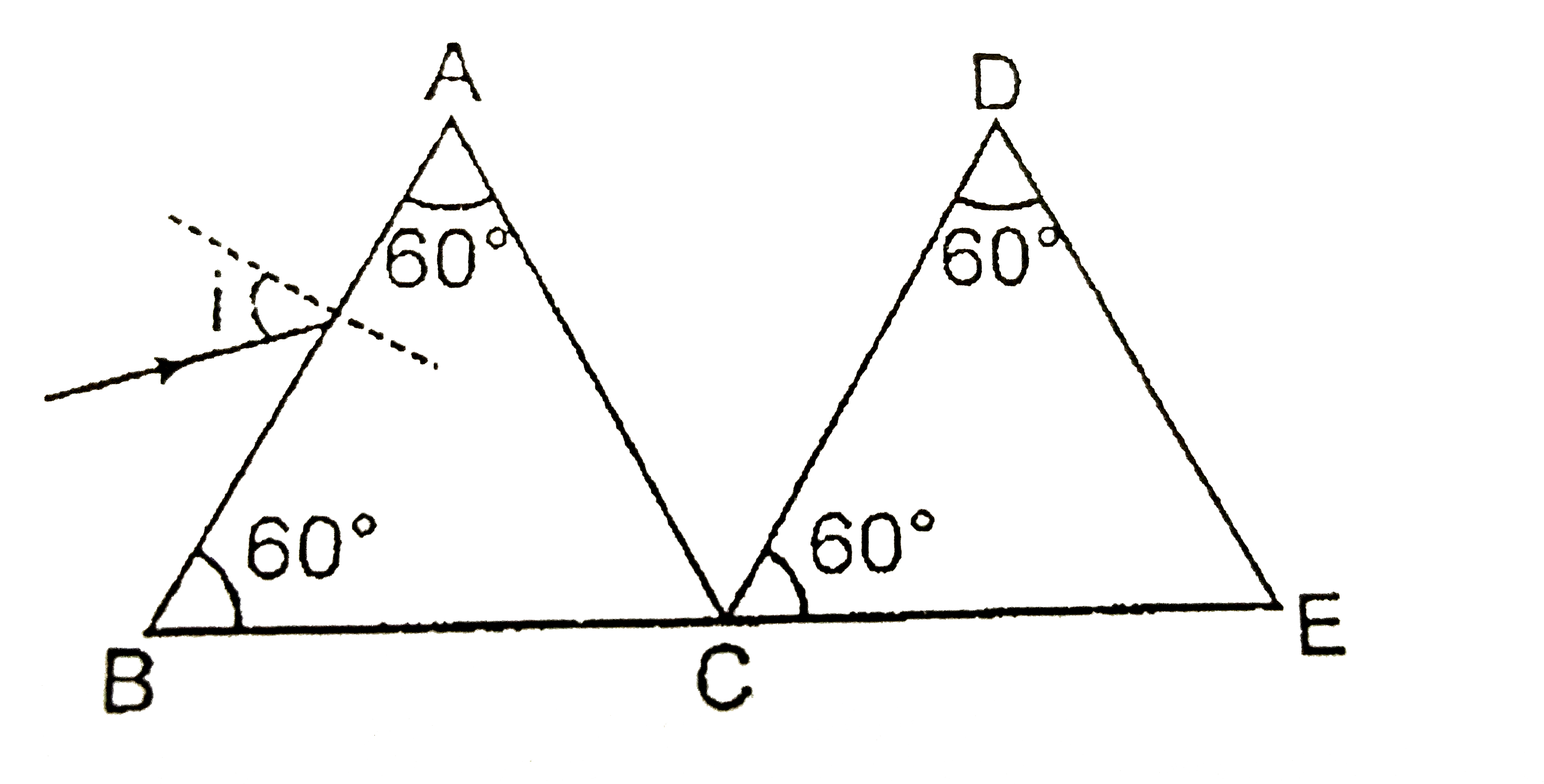
In the figure two triangular prism are shown each of refractive index √3 .
(a) Find the angle of incidence on the face AB for minimum deviation from the prism ABC ?
(b) Find the angle through which the prism DCE should be ratated about the edge passing through point C so that there should be minimum deviation from the system ?
View SolutionA ray of light is incident on a prism ABC of μ=√3 as shown in Fig. Find the angle of incidence for which the deviation of light by the prism ABC is minimum.
By what angle should the second prism be rotated so that final ray suffers net minimum deviation ?

View Solution
Knowledge Check
A light ray of angles of incidence 40∘ emerged from the prism in minimum deviation position. Then what is the angle of incidence on the second surface ?
A90∘B0∘C40∘D20∘The angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘. If the ray suffers minimum deviation through the prism, then the angle of minimum deviation is:
A30∘B60∘C45∘D90∘A ray of light passes through an equilateral prism such that the angle of incidence is equal of emergence and later is equal to 3/4th the angle of prism. The angle of deviation is
A45∘B20∘C39∘D30∘
Are the incident of emergent rays symmetrical with respect to the base of a prism in minimum deviation position ?
View SolutionA prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionRays of light pass through an equilateral prism such that the angle of incidence is equal to the angle of emergence and the latter is equal three-fourths the angle of the prism. The angle of deviation is
View SolutionLight falls on a prism grazing along first surface of a prism and the emergent ray is normal to the 2nd face of the prism. If D is angle of deviation then the refracting angle of the prism i
View Solution
