A convex lens of focal length $15 c m$ , and a concave mirror of radius of curvature $20 c m$ are placed co-axially $10 c m$ apart. An object is placed in front of convex lens so that there is no parallax between the object and its image formed by the combination. Find the position of the object.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:At $30 c m$ from lens

The given set up is shown in Fig. Here, focal length of lens, $f = 15 c m$ , radius of curvature of concave mirror, $R = 20 c m$ and $C P = 10 c m$ . Let the object be at $O$ , where $C O = u$ . As there is no parallax between the object and its image formed by the combination, therefore, final image must be at $O$ itself. For this to happens, rays refracted from convex lens $L$ must tens to meet at $I_{1}$ , the centre of curvature of concave mirror. These rays would fall normally on concave mirror and retrace their path on reflection.

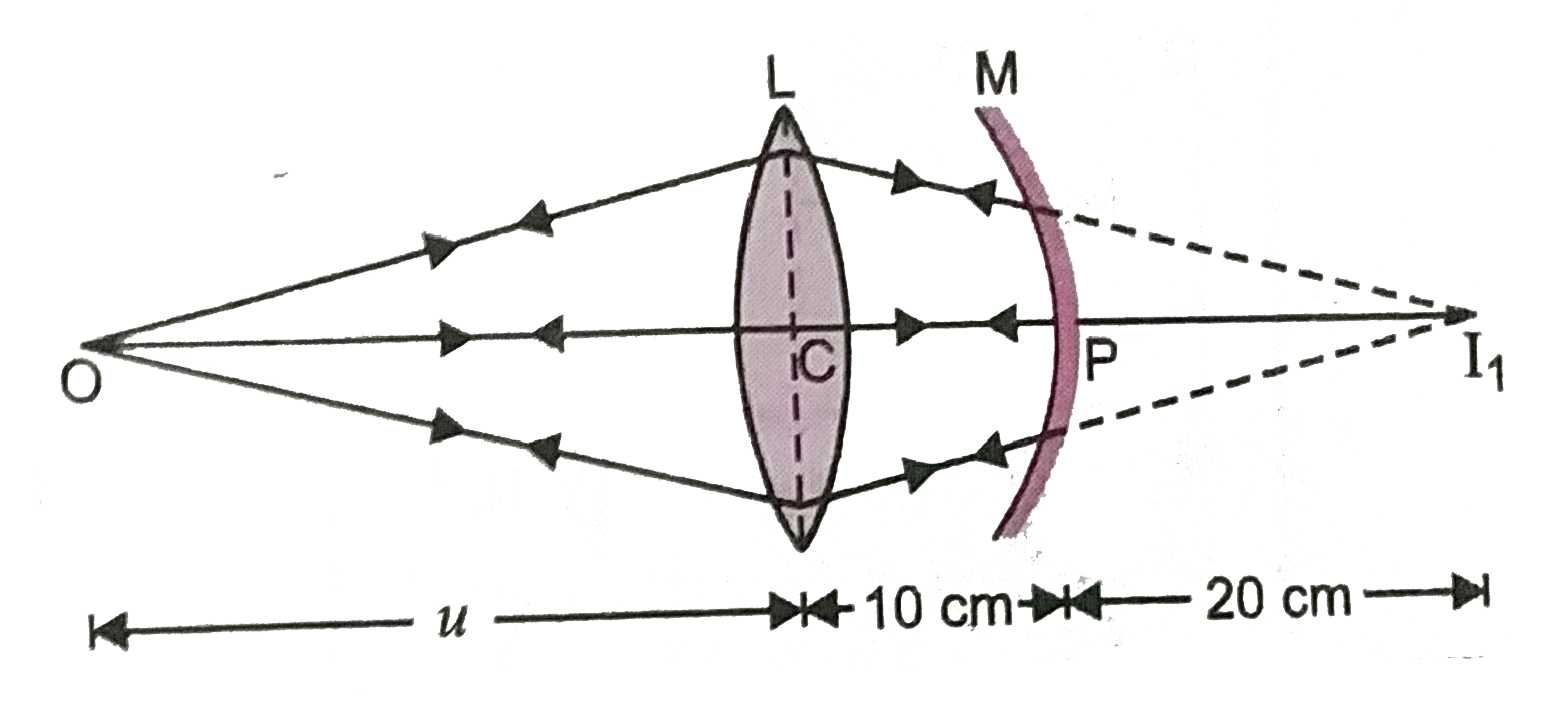
$∴ P I_{1} = R = 20 c m$ .
For the lens,
$v = C I_{1} = C P + P I_{1} = 10 + 20 = 30 c m$ .
From $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
$- \frac{1}{u} = \frac{1}{f} - \frac{1}{v} = \frac{1}{15} - \frac{1}{30} = \frac{1}{30}$
$∴ u = - 30 c m$ , i.e., $C O = 30 c m$
i.e., object must be at $30 c m$ in front of convex lens.

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What is the value of x (in cm ) so that images from by both the lenses coincides ?
A $20 (\sqrt{3} - 1)$ and $\frac{1}{\sqrt{3}}$
B $10 (\sqrt{3} - 1)$
C $\frac{20}{\sqrt{3}}$
Dnone of these

PRADEEP-OPTICS-Exercise

Home
Ask Doubt
Profile