Let A0 be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) against ln(n)
will be a circle
will be a monotonically increasing non-linear curve
will be a straight line with slope 4
will pass through the origin
The correct Answer is:C, D
As r∝n2∴AnA1=n41
ln(AnA1)=4ln(n).
The graph of ln(AnA1) against In (n) will be a straight line with slope =4. Also, it will pass through the origin.
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Fill in the blank 2
1 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Multiple choice questions 1
1 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - curiocity quetions 3
1 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
Similar Questions
The figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
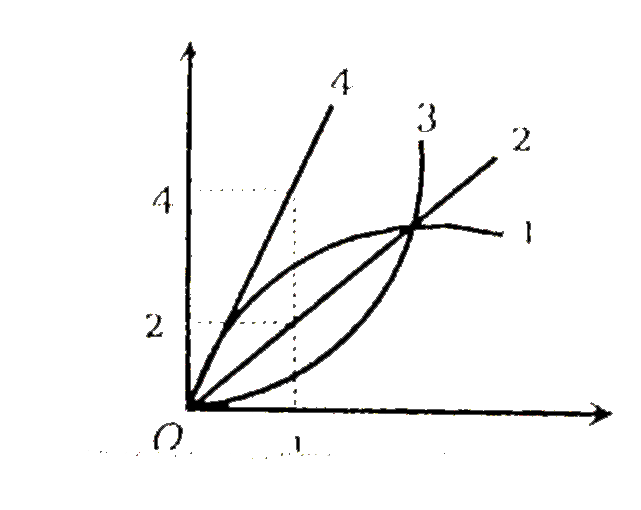
View SolutionFor a H-like species if area A1 is of ground state orbit and area An is of nth orbit, then, the plot of AnA1 us n2 looks like:
View Solution
Knowledge Check
Let A_(0) be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) againest in(pi)
Awill pass through the originBwill be a straigth line with slope 4Cwill be a monotonically increasing nonlinear curveDwill be a circleLet An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln(An/At) against In (n)
Awill pass through the originBwill have certain point lying on a straight line with slope 4Cwill be a monotonically increasing nonlinear curveDwill be a circleIn hydrogen atom, the area enclosed by nth orbit is An. The graph between log (AnA1) log will be
A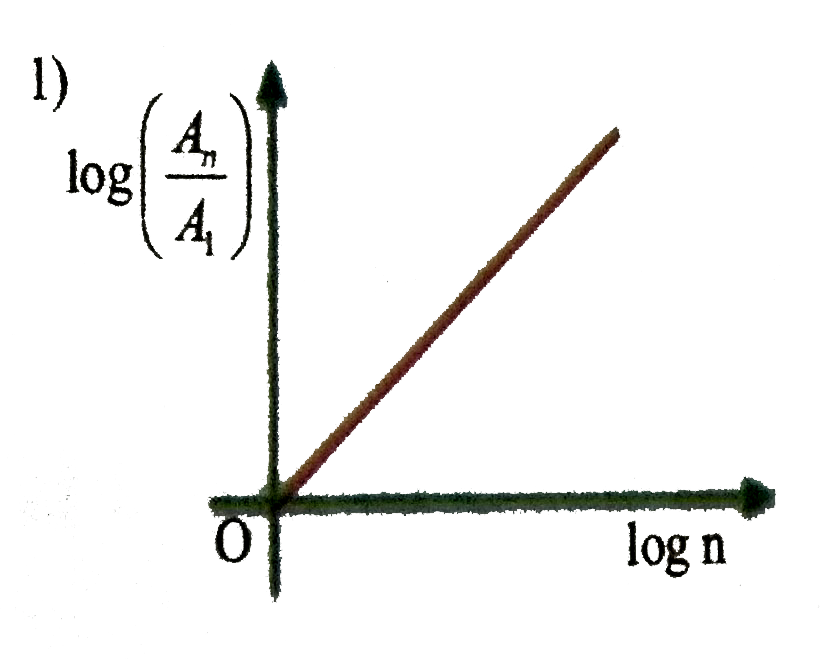 B
B C
C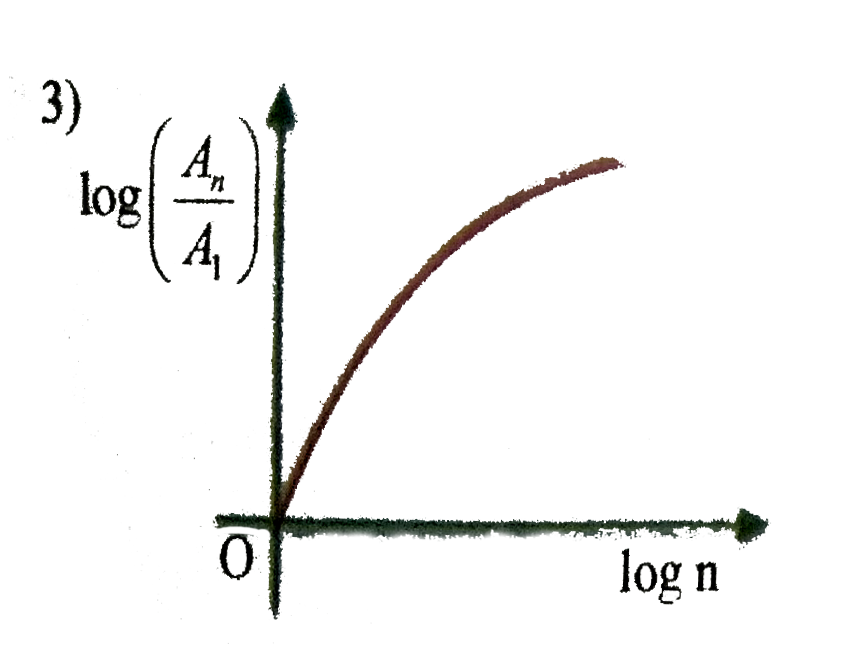 D
D
The magnitude of acceleration of the electron in the nth orbit of hydrogen atom is aH and that of singly ionized helium atom is aHe. The ratio aH:aHe is
View SolutionLet a0=0 and an=3an−1+1 for n≥1. Then the remainder obtained dividing a2010 by 11 is -
View SolutionLet a1,a2,a3 …. an be in G.P. If the area bounded by the curve y2=4anX and y2=4an(an−x) be An, then the sequence A1,A2,A3…….An are in
View SolutionLet A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1,A0A2andA0A4 is
View SolutionLet a0=0 and an=3an−1+1 for n≥1. Then the remainder obtained dividing a2010 by 11 is
View Solution
