Let A, B and C be any three logic variables, prove the following Boolean identity.
A.B.C+A.¯¯¯B.C+A.B.¯¯¯C=A.(B+C)
Taking L.H.S. of the given identy, we have
=A.B.C+¯¯¯B.C+B.¯¯¯C
=A.(B.C+¯¯¯B.C+¯¯¯B.C]
=A.[B.(C+¯¯¯C)+¯¯¯B.C]
=A.[B.(1)+¯¯¯B.C]=A.[B+¯¯¯B.C]
(∵C+¯¯¯C=1)
=A.(B+C)(∵B+¯¯¯B.C=B+C)
Which is the right hand side of the gives identity.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - SAMPLE PROBLEM2videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - CONCEPTUAL PROBLEMS1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
Similar Questions
Establish the Boolean identity
A.C+A.B.C=A.CView SolutionEstablish the Boolean identity
A.B+A.B.C+¯.B+A.¯.C=B+A.CView SolutionIn any triangle ABC , prove that following: bsinB−csinC=asin(B−C)
View SolutionIn any triangle ABC , prove that following: bcosB+c cos C=acos(B−C)
View SolutionIn any triangle ABC , prove that following : (a−b)cos(C2)=csin(A−B2)
View SolutionIn any triangle ABC , prove that following: a2sin(B−C)=(b2−c2)sinA
View SolutionIn any triangle ABC , prove that following: sin(B−C2)=b−cacosA2
View SolutionIn any triangle ABC , prove that following: a (cosBcosC+cosA)=b(cosC cosA+cosB)=c(cosA cosB+cosC).
View SolutionIn any triangle ABC , prove that following: a(sinB−sinC)+b(sinC−sinA)+c(sinA−sinB)=0
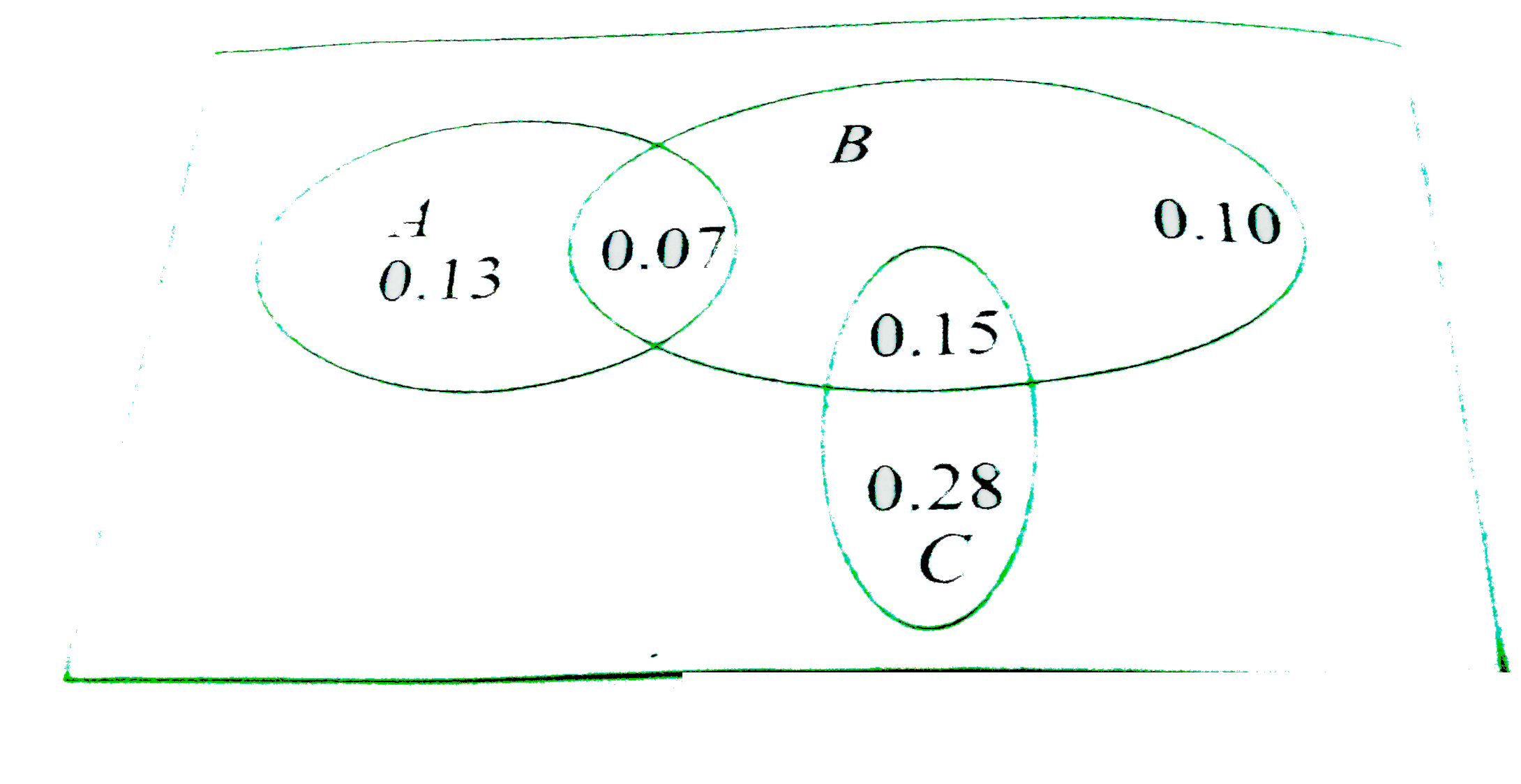
View SolutionThe following Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections.
Determine
(a) P(A)
(b) P(B∩¯¯¯C)
(c ) P(A∪B)
(d) P(A∩¯¯¯B)
(e) P(B∩C)
(f) Probability of the event that exactly one of A, B, and C occurs.
 View Solution
View Solution

