All the 7 digit numbers containing each of the digits 1,2,3,4, 5, 6,7 exactly once, and not divisible by5 are arranged in the increasing order. Find the (2004)th number in this list.
Step by step video & image solution for All the 7 digit numbers containing each of the digits 1,2,3,4, 5, 6,7 exactly once, and not divisible by5 are arranged in the increasing order. Find the (2004)^(th) number in this list. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
All the 7 digit numbers containing each of the digits 1,2,3,4, 5, 6,7 exactly once, and not divisible by5 are arranged in the increasing order. Find the (2004)th number in this list.
View SolutionAll the 7-digit numbers containing each of the digits 1,2,3,4,5,6,7 exactly once, and not divisible by 5, are arranged in increasing order. Find the 3200th number in the list
View Solution
Knowledge Check
The number of 3- digit numbers containing the digit 7 exactly once :
A225B220C200D180
All the 7-digit numbers containing each of the digits 1,2,3,4,5,6,7 exactly once, and not divisible by 5, are arranged in increasing order. Find the 2000th number in the list
View SolutionConsider all the 7-digit numbers containing each of the digits 1,2,3,4,5,6,7 exactly once, and not divisible by 5. Arrange them in decreasing order. What is the 2015-th number (from the beginning) in this list?
View SolutionThe number of 3- digit numbers containing the digit 7 exactly once :
View SolutionAll the five digit numbers in which each successive digit exceeds its predecessor are arranged in the increasing order of their magnitude. The 97th number in the list does not contain the digit
View SolutionAll the five digit numbers in which each successive digit exceeds its predecessor are arranged in the increasing order of their magnitude. The 97th number in the list does not contain the digit
View SolutionUsing digits 2,4,7 and 8 exactly once, find the smallest 4-digit number divisible by 4
View SolutionUsing the digits 1, 2, 3, 4, 5, 6,7, a number of 4 different digits is formed. Find
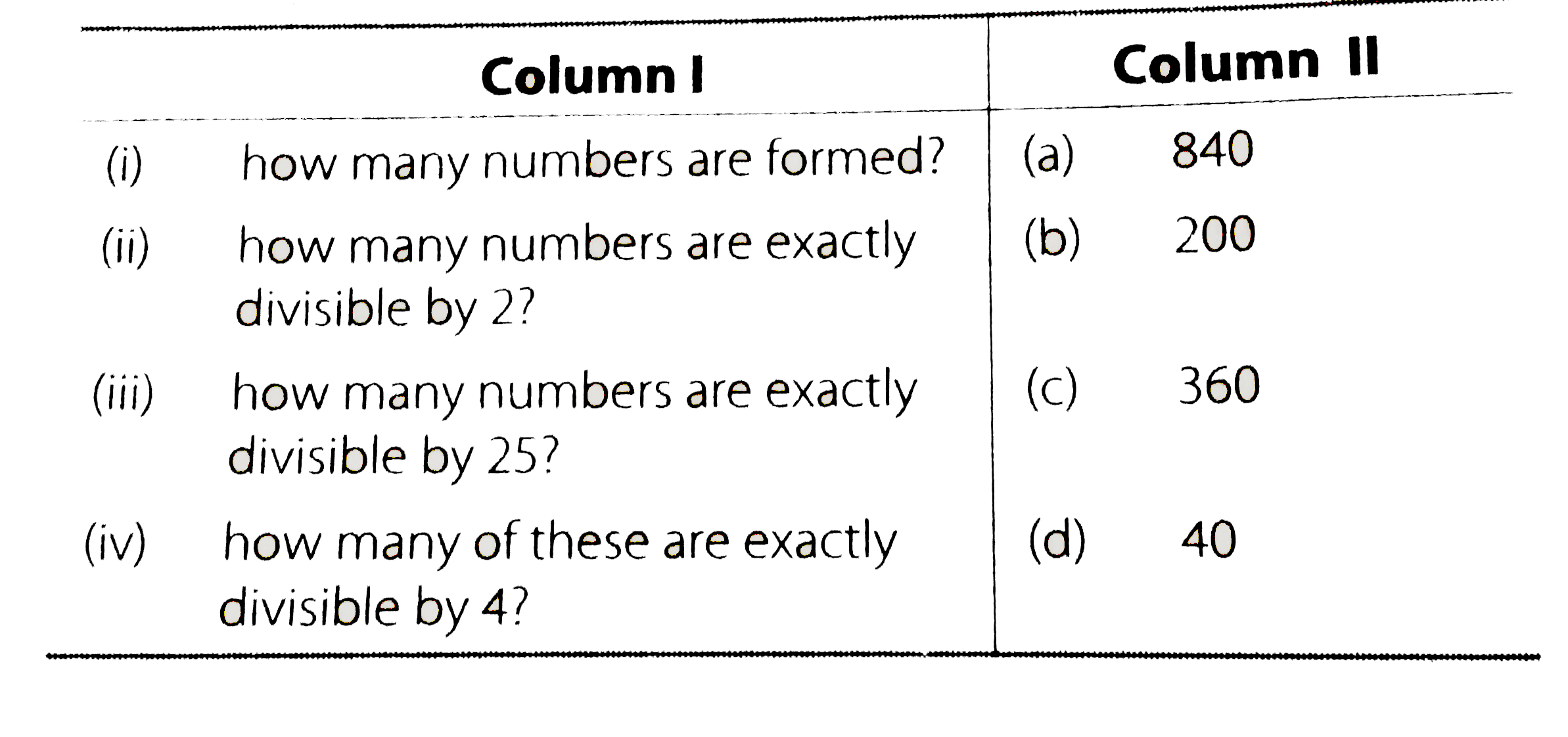
View Solution
