If the graph of the function y = f(x) passes through the points (1, 2) and (3, 5), then ∫31f'(x)dx=
1
2
3
4
The correct Answer is:C
Step by step video, text & image solution for If the graph of the function y = f(x) passes through the points (1, 2) and (3, 5), then int_(1)^(3)f'(x) dx= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - MULTIPLE CHOICE QUESTIONS (PREVIOUS YEARS (MHT-CET EXAM QUESTIONS))12videos
INTEGRATION - DEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - DEFINITE INTEGRALS EXERCISE - TEST YOUR GRASP20videos
INTEGRATION - DEFINITE INTEGRALS
- BOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 11)24videos
DIFFERENTIATION
- BOOK - MARVEL PUBLICATIONCHAPTER - INTEGRATION - INDEFINITE INTEGRALSEXERCISE - TEST YOUR GRASP45videos
INTEGRATION - INDEFINITE INTEGRALS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The graph of the function y = f(x) passing through the point (0, 1) and satisfying the differential equation dydx+ycosx=cosx is such that
Ait is a differential function ∀x∈RBIt is continuous ∀x∈RCIt is periodicDIt is passing through (π,1) - Question 2 - Select One
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA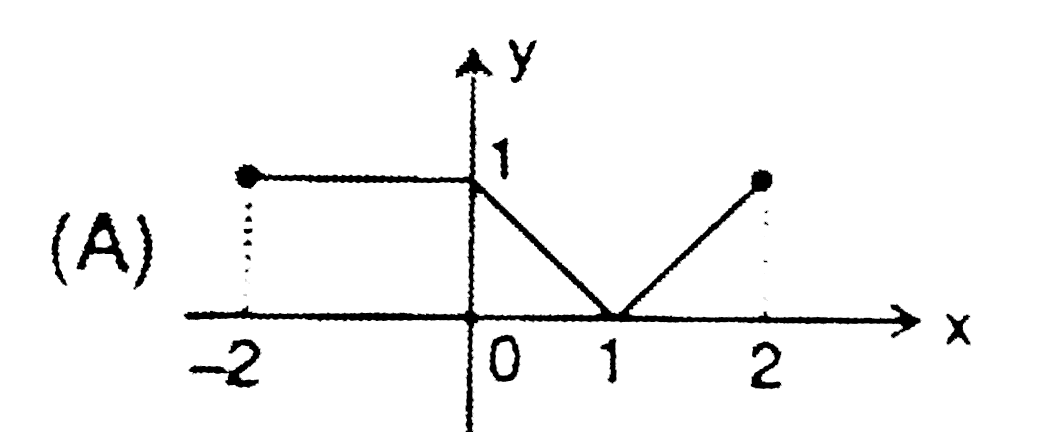 B
B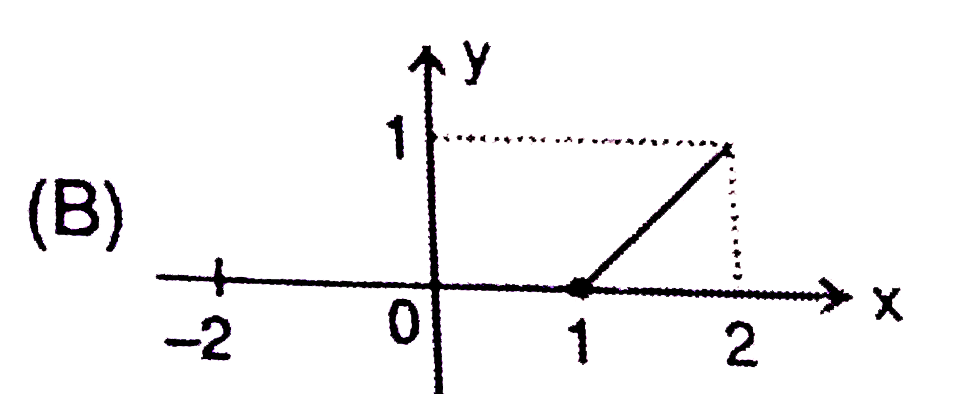 C
C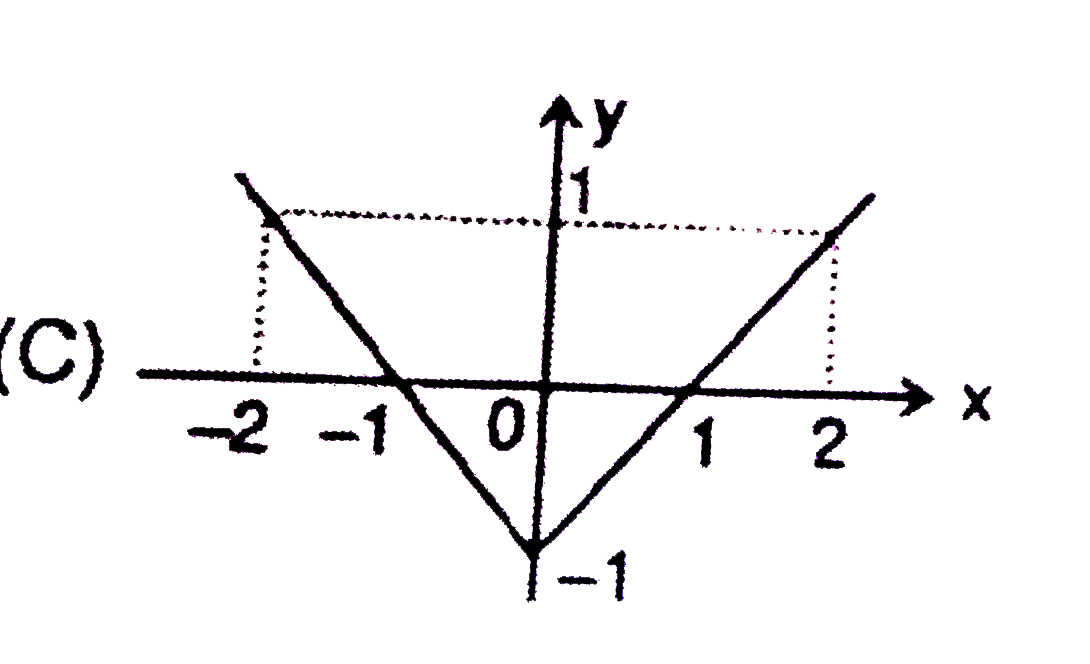 D
D
- Question 3 - Select One
Suppose that the graph of y=f(x), contains the points (0,4)and(2,7). If f' is continuous then ∫20f'(x)dx is equal to
A2B−2C3Dnone of these
The tangent, represented by the graph of the function y=f(x), at the point with abscissa x = 1 form an angle of π/6, at the point x = 2 form an angle of π/3 and at the point x = 3 form and angle of π/4. Then, find the value of,
∫31f'(x)f''(x)dx+∫32f''(x)dx.View SolutionIf the curve y=f(x) passing through the point (1,2) and satisfies the differential equation xdy+(y+x3y2)dx=0 ,then
View SolutionThe tangent to the graph of the function y=f(x) at the point with abscissa x=a forms with the x-axis an angle of π3 and at the point with abscissa x=b at an angle of π4, then the value of the integral, ∫b1f'(x).f''(x)dx is equal to
View SolutionIf the graph of the function y=f(x) has a unique tangent at the point (a,0) through which the graph passes, then evaluate (lim)x→a(log)e{1+6f(x)}3f(x)
View SolutionA line tangent to the graph of the function y=f(x) at the point x = a forms an angle π3 with the axis of Abscissa and angle π4 at the point x=b then ∫baf''(x)dx is
View Solution

