Particles of masses 2M, m and M are respectively at points A, B and C with AB=12 (BC). M is much smaller than M and at time t = 0, they are all at rest given in the figure. At subsequent times before any collision takes place.
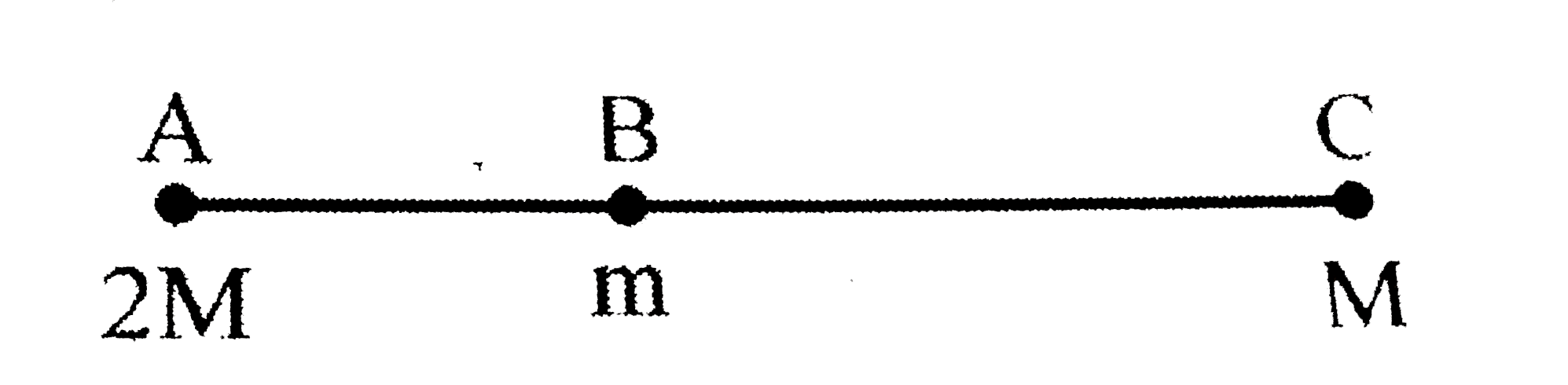
m will remain at rest
m will move towards M
m will move towards 2 M
m will have oscillatory motion
The correct Answer is:C
Gravitational force on m due to 2M=FBA
=G(2M)m(AB)2 along −−→BA …. (1)
Gravitational force on m due to M=FBC
=G(M)m(BC)2 along −−→BC
∵BC=2AB ∴ FBC=GMm4AB2 ...... (2)
Thus from (1) and (2) we find that FBA>FBC
∴ m will move towards 2M along −−→BA.
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
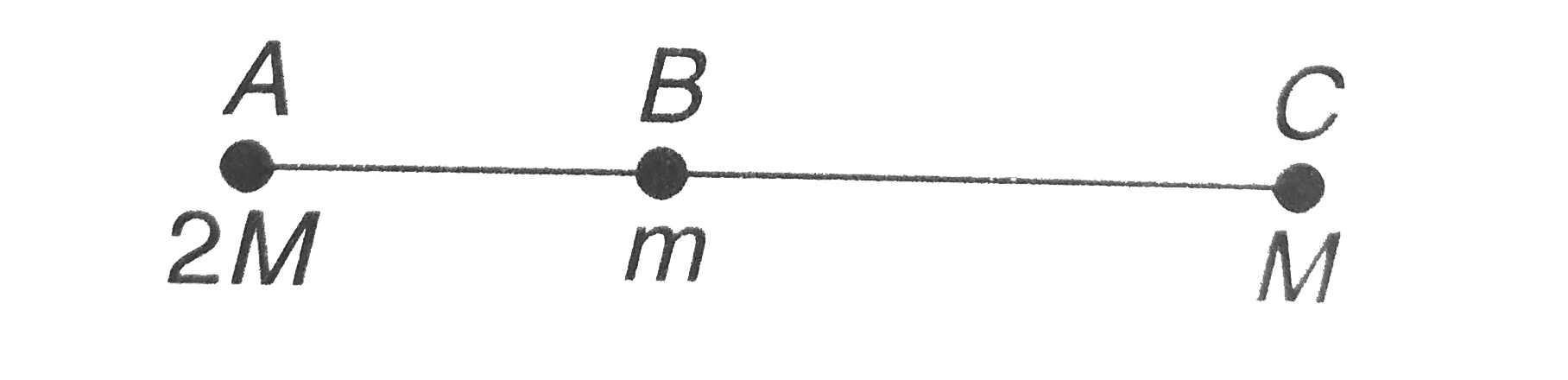
View Solutionparticles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .

View Solution
Knowledge Check
particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
 Am will remain at restBm will move towards MCm will move towards 2MDm will have oscillatory motion
Am will remain at restBm will move towards MCm will move towards 2MDm will have oscillatory motionParticles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
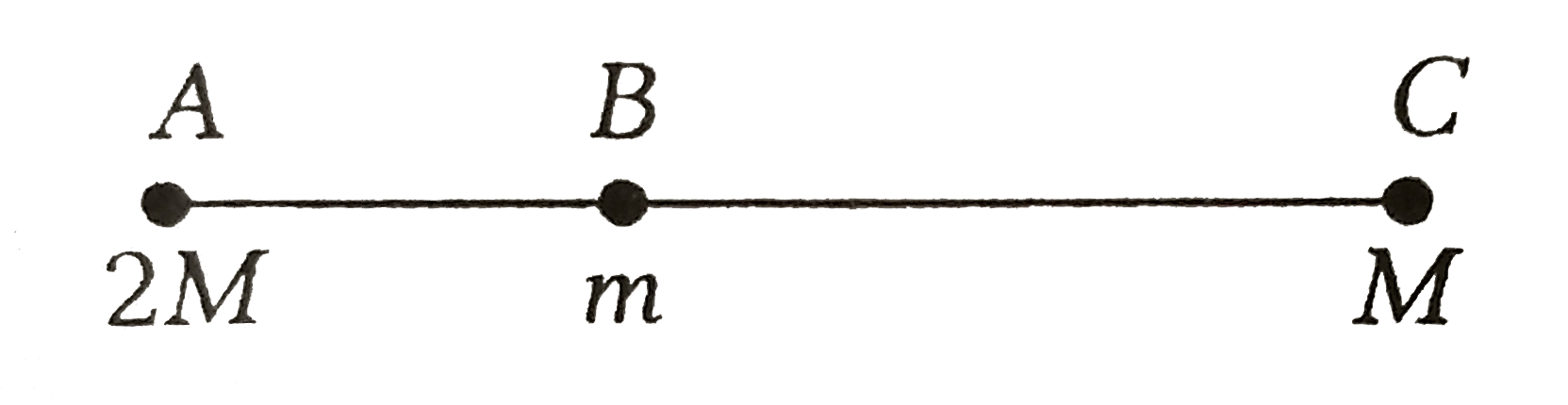
At subsequent time before any collision takes place.Am will remain at restBm will move towards MCm will move towards 2MDm will have oscillatory motionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)A2ms−1B1.25ms−1C2.5ms−1D5ms−1
Particles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
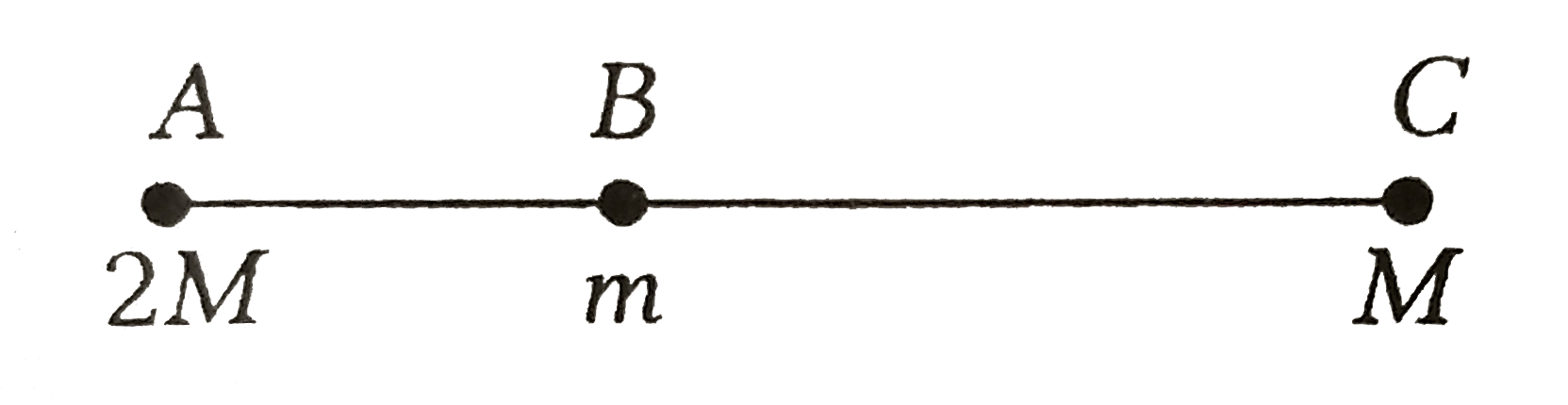
At subsequent time before any collision takes place.
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)
View SolutionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View SolutionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
View Solution
