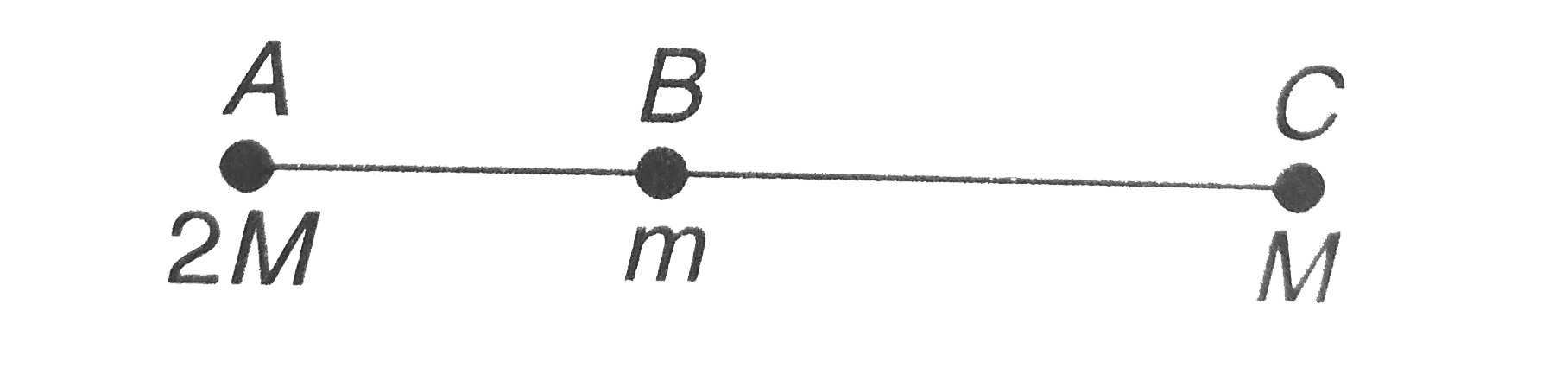
particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
The correct Answer is:C
( c) 
Force on mass m at B due to mass M at C is
F1=Gm×2M(AB)2 along BA
Force on mass m at B due to mass M at C is
F2=GmM(BC)2 along BC
∴ Resultant force on mass ma at B due to masses at A and C is
FR=F1−F2 ( ∴F1 and F2 are acting in opposite direction )
=2GmM(AB)2−GmM(BC)2
∵AB=12BC
∴FR=2GmM(12BC)2⎞⎟
⎟⎠−GmM(BC)2 along BA
=8GmM(BC)2−GmM(BC)2 along BA
=7GmM(BC)2 along BA
Therefore, m will towards 2M.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion & Reason Corner15videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Kepler Laws17videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - HOTS10videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Particles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
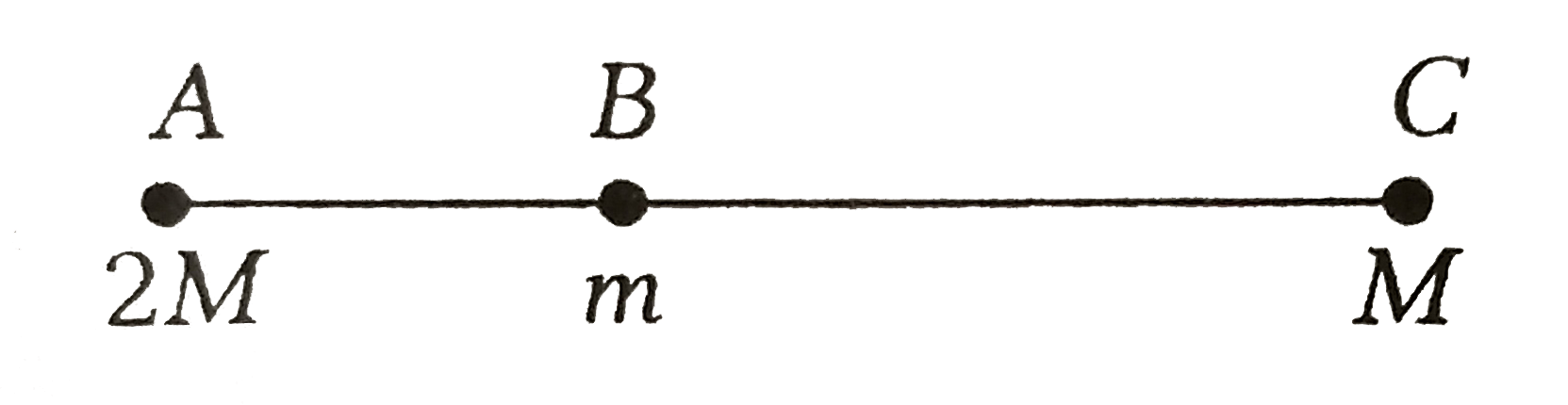
At subsequent time before any collision takes place.View SolutionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png) View Solution
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)View Solutionconsider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same direction. The collision starts at t=0 and the particles interact for a time interval △t. during the collision the speed of the first particle varies as
v(t)=u1+t/ t(v1−u1) Find the speed of the second particle as as function of time during the collision.View SolutionTwo particles of masses m1 and m2 and velocities u1 and αu1(α≠0) make an elastic head on collision. If the initial kinetic energies of the two particles are equal and m1 comes to rest after collision, then
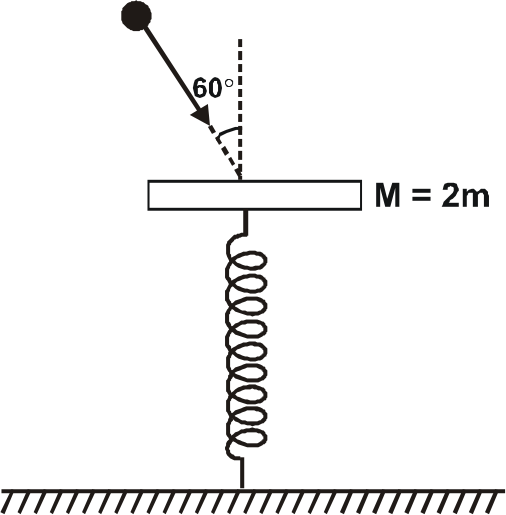
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
Minimum kinetic energy of the particle after collision isView SolutionAt time t=0, a particle is at (−1m,2m) and at t=2s it is at (−4m,6m). From this we can conclude that in the given time interval.
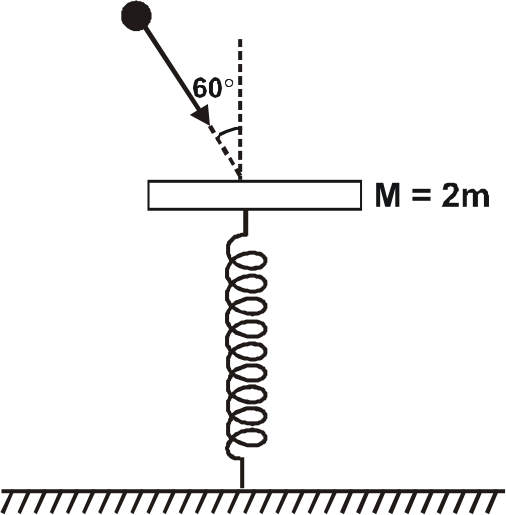
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
Maximum compression in the spring after the collision theView SolutionTwo particles A and B are revolving with constant angular velocity on two concentric circles of radius 1m and 2m respectively as shown in figure. The positions of the particles at t = 0 are shown in figure. The positions of the particles at t=0 are shown in figure. if mA=2kg,mB=1kg and →PA and →PB are linear momentum of the particle then what is the maximum value of ∣∣→PA+→PB∣∣ in kg-m/sec in subsequent motion of two particles.
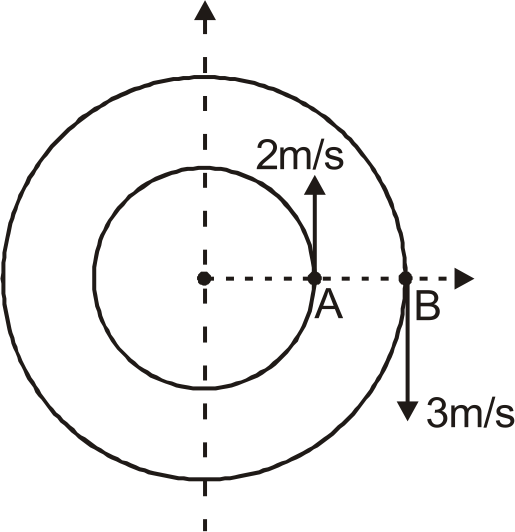 View Solution
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View Solution

