If an alternating e.m.f. is applied to a series L-R circuit, the phase angle between e.m.f. and current is given by tanθ=ωLR. Hence the power factor of the series L-R circuit is
1. ωLR
2. RωL
3. RR+ωL
4.R√R2+ω2L2
The correct Answer is:D
tanθ=LωR
∴ Power factor = cosθ=R√R2+L2ω2

Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 1630videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 515videos
ELASTICITY
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The current in the series L-C-R circuit is
Ai=imsin(ωt+ϕ)Bi=vm√R2+(Xc−XL)2sin(ωt+ϕ)Ci=2imcos(ωt+ϕ)DBoth (a) and (b) - Question 2 - Select One
The phase angle between e.m.f. and current in LCR series ac circuit is
A0 to π/2Bπ/4Cπ/2Dπ - Question 3 - Select One
In L−C−R series circuit
Acurrent may achieve same value for two different value of frequencyBcurrent can not achieve same value for two different values of frequencyCcurrent is maximum for a maximum value of frequencyDnone of these
For an A.C. Circuit, contianing a resistance and a capacitance in series, the angle between current and e.m.f. is given by tanθ=1(ωCR). The power factor of this circuit is
View SolutionAt resonance of the given series R−L−C circuit:
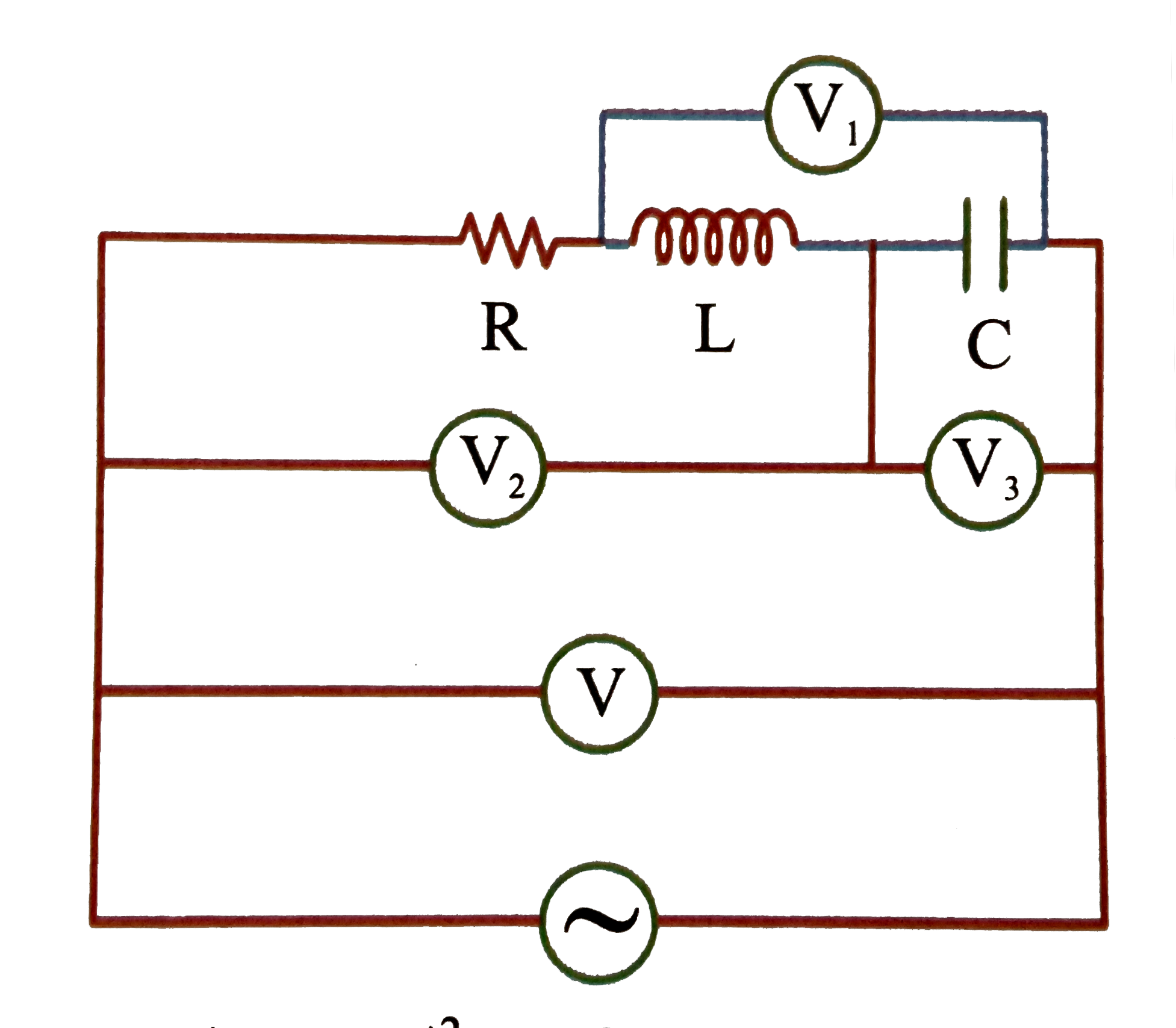 View Solution
View SolutionFor a series L C R circuit, the power loss at resonance is
View SolutionAn alternating e.m.f. is applied to purely capacitive circuit. The phase relation between e.m.f. and current flowing in the circuit is or in a circuit containing capacitance only
View SolutionAn alternating e.m.f. is applied to a series L-C-R circuit. If the frequency of the applied e.m.f. is more than the resonant frequency of the circuit then the circuit will act as
View Solution

