The M.I. of a rectangular plane lamina of mass M, length 'l' and breadth 'b' about an axis passing through its centre and perpendicular to plane of lamina is
Ml212
Mb212
M(l2+b2)12
M12(l2b2+b24)
The correct Answer is:C
To find the moment of inertia (M.I.) of a rectangular plane lamina of mass M, length l, and breadth b about an axis passing through its center and perpendicular to the plane of the lamina, we can follow these steps:
1. Understand the Geometry:
- We have a rectangular lamina with length l and breadth b. The mass of the lamina is M.
- The axis of rotation is perpendicular to the plane of the lamina and passes through its center.
2. Use the Formula for Moment of Inertia:
- The moment of inertia I for a rectangular lamina about an axis perpendicular to its plane and passing through its center is given by the formula:
I=112M(l2+b2)
- This formula is derived from the integration of the mass distribution over the area of the rectangle.
3. Substitute Values:
- Substitute the values of M, l, and b into the formula:
I=112M(l2+b2)
4. Final Result:
- Therefore, the moment of inertia of the rectangular lamina about the specified axis is:
I=112M(l2+b2)
- We have a rectangular lamina with length l and breadth b. The mass of the lamina is M.
- The axis of rotation is perpendicular to the plane of the lamina and passes through its center.
- The moment of inertia I for a rectangular lamina about an axis perpendicular to its plane and passing through its center is given by the formula:
I=112M(l2+b2)
- This formula is derived from the integration of the mass distribution over the area of the rectangle.
- Substitute the values of M, l, and b into the formula:
I=112M(l2+b2)
- Therefore, the moment of inertia of the rectangular lamina about the specified axis is:
I=112M(l2+b2)
Topper's Solved these Questions
Similar Questions
Find the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
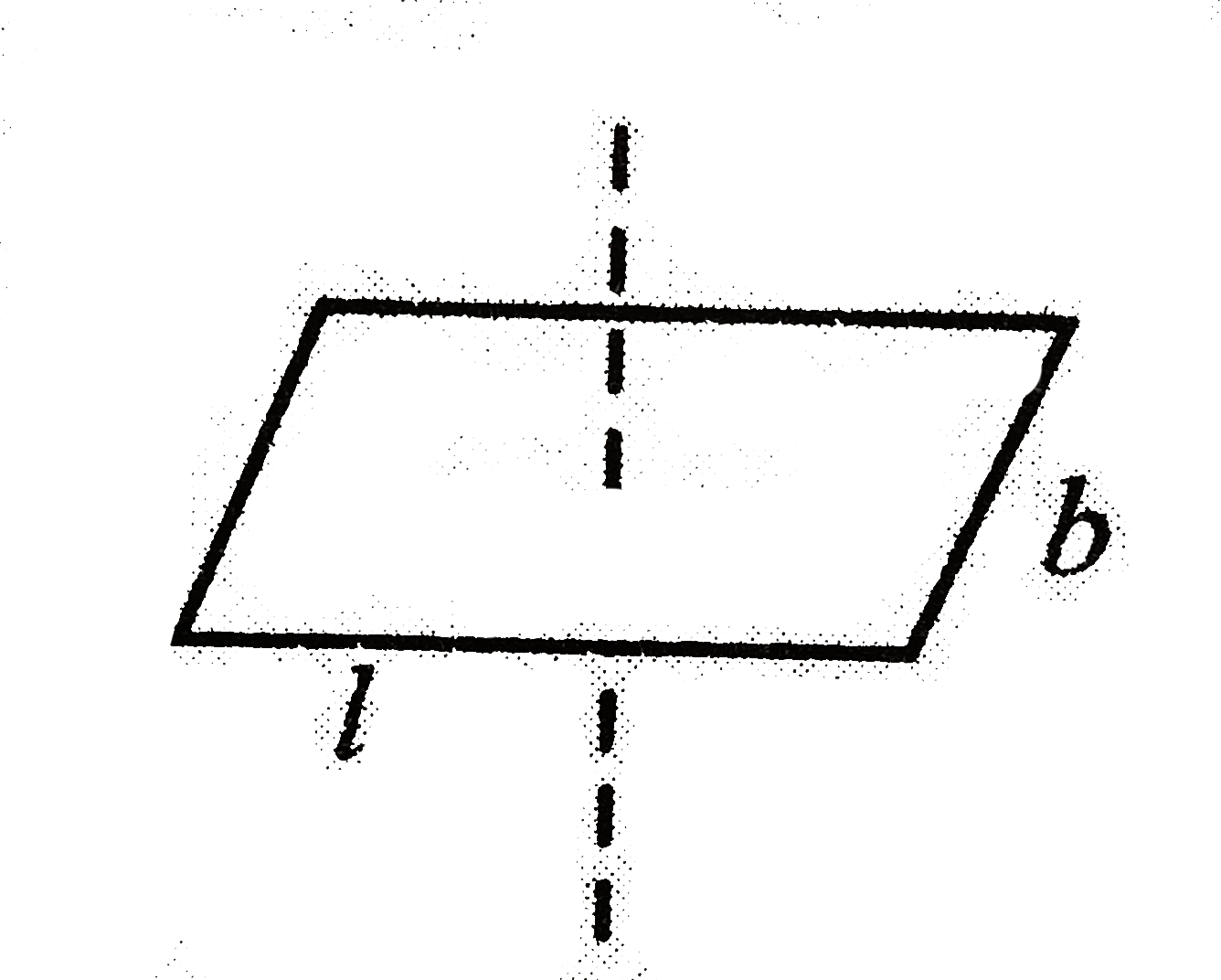 View Solution
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2 - Question 2 - Select One
The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
AMl2BMl2/3CMl2/2DMl2/12 - Question 3 - Select One
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2R
Calculate the moment of inertia of a rectangular frame formed by uniform rods having mass m each as shown in about an axis passing through its centre and perpendicular to the plane of frame. Also find moment of inertia about an axis passing through PQ ?
 View Solution
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
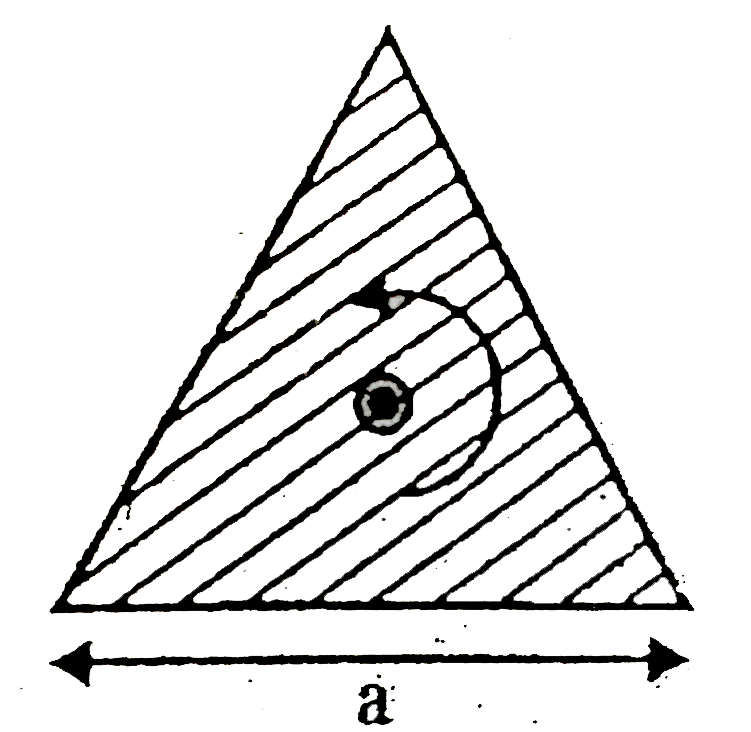
View SolutionA unifor4m equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
 View Solution
View SolutionThe M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
View Solution

