The ratio of the maximum velocity and maximum displacement of a particle executing simple harmonic motion is equal to
A
ω
B
T
C
g
D
n
Video Solution
Text Solution
The correct Answer is:A
vmxm=AωA=ω.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2 - Question 2 - Select One
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.Dits linear velocity and acceleration always attain their peak values simlataneaously. - Question 3 - Select One or More
The phase of a particle executing simple harmonic motion is π2 when it has
AMaximum velocityBMaximum accelerationCMaximum energyDMaximum displacement
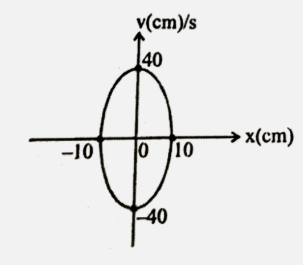
Figure shows the graph of velocity versus displacement of a partciel executing simple harmonic motion. Find the period of oscillation of the particle.
 View Solution
View SolutionIf a body is executing simple harmonic motion, then
View SolutionThe shape of graph plotted between velocity and position of a particle executing simple harmonic motion is
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View SolutionThe phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is
View Solution