The equation of a simple harmonic progressive wave along the negative direction of X-axis is
y=asin2π[tT−xλ]
y=asin(2πnt)
y=asin2π[tT+xλ]
y=acos2π[x]
The correct Answer is:C
To find the equation of a simple harmonic progressive wave traveling along the negative direction of the X-axis, we can follow these steps:
Step 1: Understand the General Equation of a Progressive Wave
The general equation for a simple harmonic wave traveling in the positive x-direction is given by:
y(x,t)=Asin(ωt−kx+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- ϕ is the phase constant.
Step 2: Modify the Equation for Negative Direction
For a wave traveling in the negative x-direction, the equation modifies to:
y(x,t)=Asin(ωt+kx+ϕ)
This change occurs because the wave is moving in the opposite direction.
Step 3: Relate Angular Frequency and Wave Number
The angular frequency ω can be expressed in terms of the frequency f and the wave number k can be expressed in terms of the wavelength λ:
- ω=2πf
- k=2πλ
Step 4: Substitute ω and k into the Equation
Substituting these values into the equation gives:
y(x,t)=Asin(2πft+2πλx+ϕ)
Step 5: Final Form of the Equation
Thus, the final form of the equation for a simple harmonic progressive wave traveling along the negative direction of the X-axis is:
y(x,t)=Asin(2πft+2πλx+ϕ)
Summary
The equation of a simple harmonic progressive wave traveling in the negative direction of the X-axis is:
y(x,t)=Asin(2πft+2πλx+ϕ)
---
The general equation for a simple harmonic wave traveling in the positive x-direction is given by:
y(x,t)=Asin(ωt−kx+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number,
- ϕ is the phase constant.
For a wave traveling in the negative x-direction, the equation modifies to:
y(x,t)=Asin(ωt+kx+ϕ)
This change occurs because the wave is moving in the opposite direction.
The angular frequency ω can be expressed in terms of the frequency f and the wave number k can be expressed in terms of the wavelength λ:
- ω=2πf
- k=2πλ
Substituting these values into the equation gives:
y(x,t)=Asin(2πft+2πλx+ϕ)
Thus, the final form of the equation for a simple harmonic progressive wave traveling along the negative direction of the X-axis is:
y(x,t)=Asin(2πft+2πλx+ϕ)
The equation of a simple harmonic progressive wave traveling in the negative direction of the X-axis is:
y(x,t)=Asin(2πft+2πλx+ϕ)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equation of a simple harmonic progressive wave along the positive direction of X axis is given by
Ay=asin2π[tT−xλ]By=asin(2πnt)Cy=asin2π[tT+xλ]Dy=acos(2πnt)The equation of a simple harmonic progressive wave having amplitude 5 mm, period 2 second and wavelength 2m and travelling along the positive direction of the x-axis is given by
Ay=5sin2π(t2−x2)By=5×10−3sin2π(2t−x2)Cy=5×10−3sin2π(t2−x2)Dy=5×10−3sinπ(2t−x)In the equation of a simple harmonic progressive wave of wavelength 'λ', the propagation constant is given by
A2π/λBπλCπ/λDλ/2π
Equation OF simple harmonic travelling wave
View SolutionDerive an expression for a one - dimensional simple harmonic progressive wave travelling in the direction of the positive x - axis. Express it in terms of A,λ, v , t and x .
View SolutionThe figure below is a representation of a simple harmonic progressive in the negative X-axis, at a given instant. The direction of the velocity of the particle at stage P in the figure is best represent by the arrow.
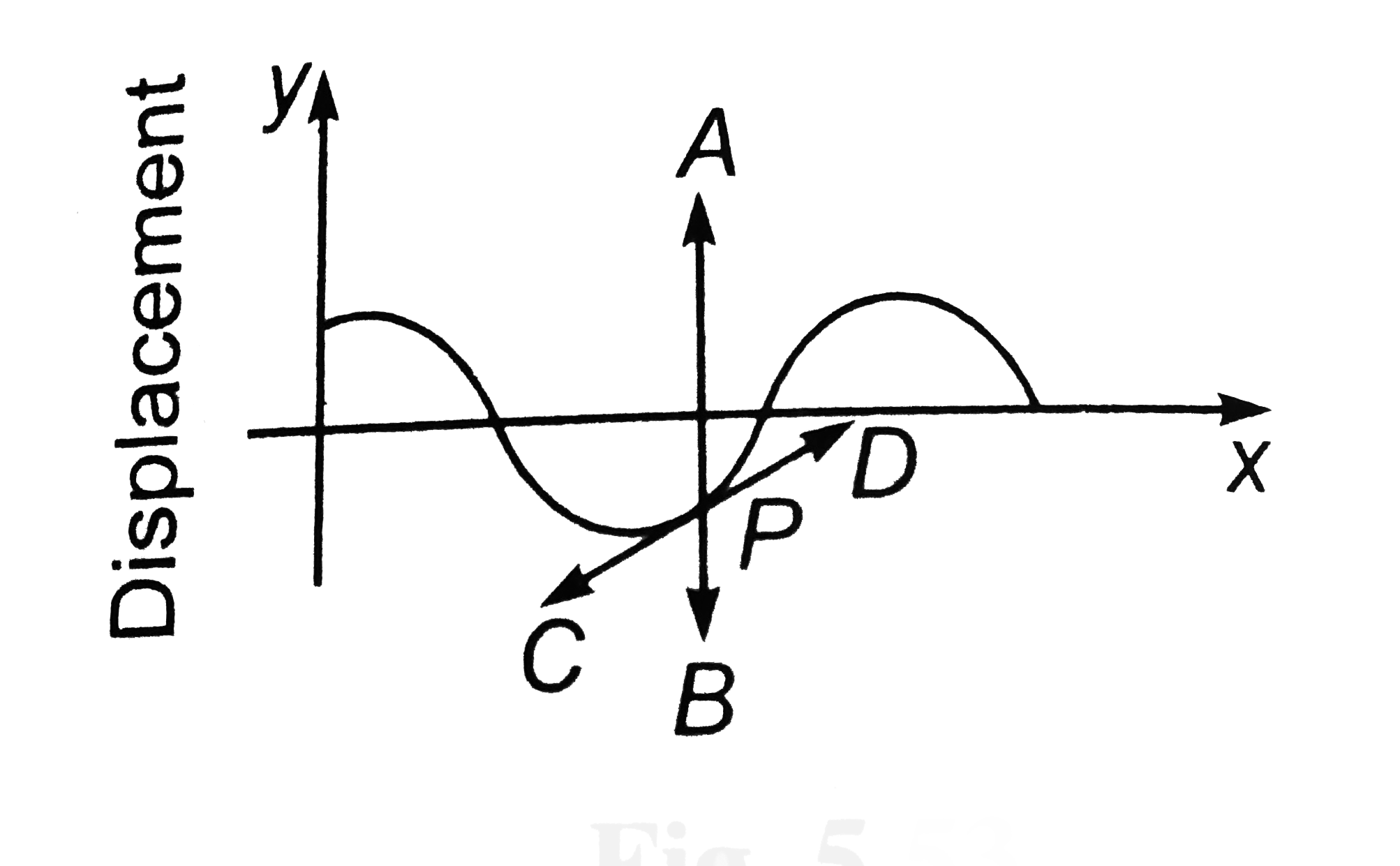
View SolutionThe equation of a simple harmonic progressive wave is given by y=12sin(ωt−4x)m. What is the distance between 2 particles on the wave, having a phase difference of π/2 ?
View SolutionThe equation of progressive wave travelling a long positive direction of x axis having a amplitude of 0.04 m, frequency 440 Hz and wave velocity 330 m/s, is
View Solution
