A beam of light is incident on glass slab making an angle of 60∘ with the surface. The angle of refraction and the velocity of light in glass of R.I. 1.5 are
19∘28,3×108m/s
29∘28',2×108m/s
19∘28',2×108m/s
29∘28,3×108m/s
The correct Answer is:C
To solve the problem, we need to find the angle of refraction and the velocity of light in the glass slab given the angle of incidence and the refractive index of the glass.
1. Identify the Given Data:
- Angle of incidence with respect to the surface = 60∘
- Refractive index of glass (n2) = 1.5
- Refractive index of air (n1) = 1 (approximately)
2. Calculate the Angle of Incidence:
- The angle of incidence (I) with respect to the normal is calculated as:
I=90∘−60∘=30∘
3. Apply Snell's Law:
- Snell's Law states:
n1sinI=n2sinR
- Substitute the known values:
1⋅sin(30∘)=1.5⋅sinR
- We know that sin(30∘)=12:
1⋅12=1.5⋅sinR
- This simplifies to:
12=1.5⋅sinR
4. Solve for sinR:
- Rearranging gives:
sinR=1/21.5=13
5. Calculate the Angle of Refraction:
- To find R, take the inverse sine:
R=sin−1(13)
- Using a calculator, we find:
R≈19∘28′
6. Calculate the Velocity of Light in Glass:
- The formula for the velocity of light in a medium is:
v=cn
- Where c is the speed of light in vacuum (3×108m/s) and n is the refractive index.
- Substitute the values:
v=3×1081.5=2×108m/s
Final Answers:
- Angle of refraction R≈19∘28′
- Velocity of light in glass v=2×108m/s
---
- Angle of incidence with respect to the surface = 60∘
- Refractive index of glass (n2) = 1.5
- Refractive index of air (n1) = 1 (approximately)
- The angle of incidence (I) with respect to the normal is calculated as:
I=90∘−60∘=30∘
- Snell's Law states:
n1sinI=n2sinR
- Substitute the known values:
1⋅sin(30∘)=1.5⋅sinR
- We know that sin(30∘)=12:
1⋅12=1.5⋅sinR
- This simplifies to:
12=1.5⋅sinR
- Rearranging gives:
sinR=1/21.5=13
- To find R, take the inverse sine:
R=sin−1(13)
- Using a calculator, we find:
R≈19∘28′
- The formula for the velocity of light in a medium is:
v=cn
- Where c is the speed of light in vacuum (3×108m/s) and n is the refractive index.
- Substitute the values:
v=3×1081.5=2×108m/s
- Angle of refraction R≈19∘28′
- Velocity of light in glass v=2×108m/s
Topper's Solved these Questions
Similar Questions
If a ray of light propagating in air strikes a glass slab at an angle of 30∘ with the surface of the slab, the angle of refraction is
View SolutionA ray of light is incident on a glass slab at the polarising angle of 58∘ . Calculate the percentage change in the speed of light in glass.
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light is incident on ice slab making an angle of 50∘ with the normal. The angle of refraction and velocity of light in ice of the refractive index 1.3 are
A35∘6',2.307×108m/sB36∘6',2.307×108m/sC36∘6',3.307×108m/sD35∘6',3.307×108m/s - Question 2 - Select One
A ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘ - Question 3 - Select One
A ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
A28∘B33∘C12∘D15∘
Light is incident on a glass slab making an angle of 30∘ with the surface. If the speed of light in air is 3×108m/s and the refractive index of glass is 1.5, find:
(i)the angle of refraction.
(ii ) the speed of light in glass.View SolutionA ray of light strikes the glass slab at an angle of 90∘ from its surface. What is the angle of incidence and the angle of refraction ?
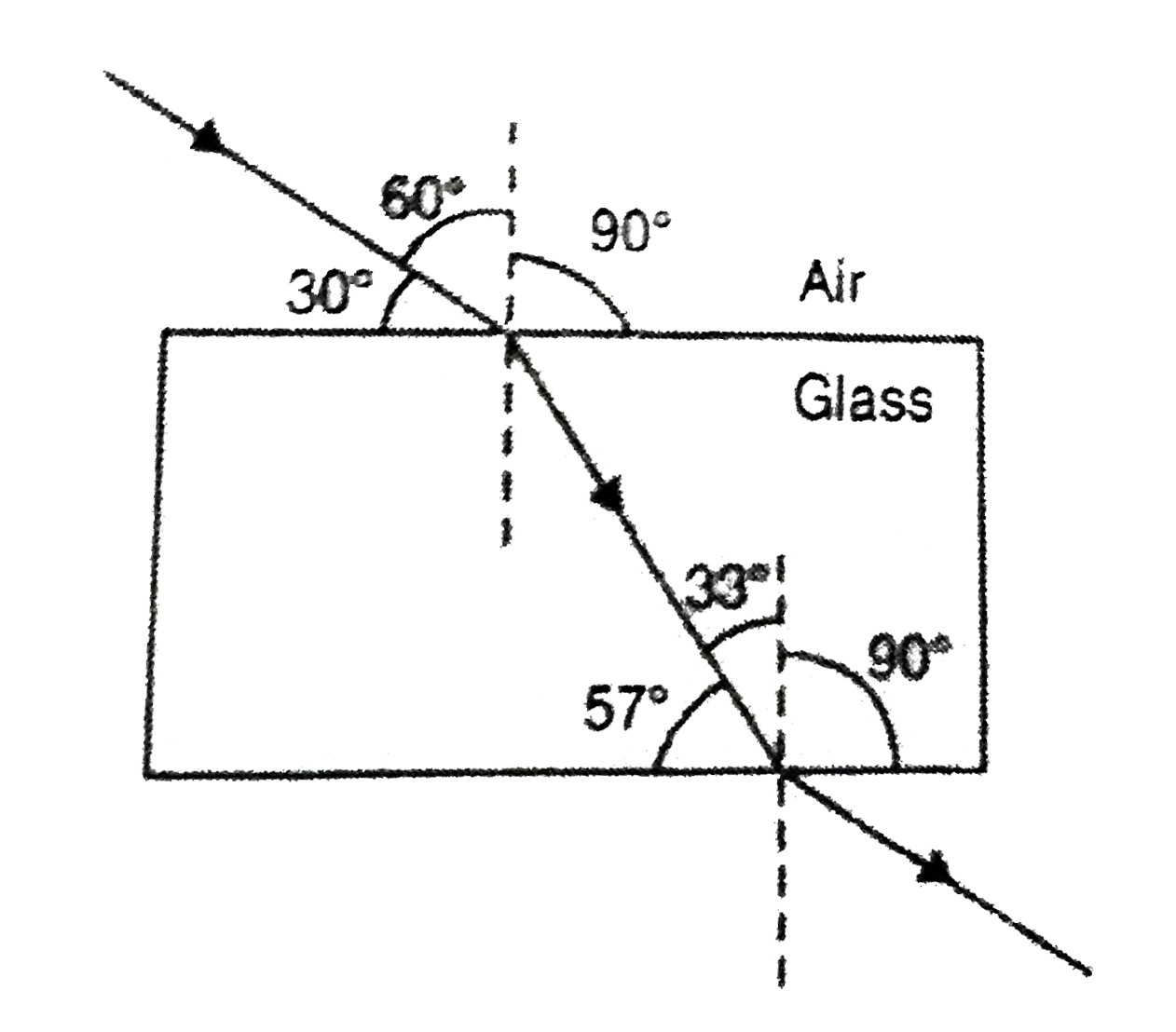
View SolutionA ray of light is incident on a galss slab making on angle of 30∘ with the surface . If the angle of refraction in glass is 33∘, the angle of deviation of the ray during its passage through the galss slab is
View SolutionA ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
View SolutionA ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
 View Solution
View Solution

