A coherent light is incident on two paralle slits S1andS2. At a point P1 the frings will be dark if the phase difference between the rays coming from S1andS2 is
nπ radians
(n+0.5)π radians
(2n+0.5)π radians
(2n+1)π radians
The correct Answer is:D
Fow destructive interference, phase difference should be odd multiple of π.
Topper's Solved these Questions
Similar Questions
Three coherent sourcesS1,S2 andS3 can throw light on a screen. With S1 switched on intensity at a point P on the screen was observed to be I. With onlyS2 on, intensity at P was 2I and when all three are switched on the intensity at P becomes zero. Intensity at P is I when S1 andS2 are kept on. Find the phase difference between the waves reaching at P from sources S1andS3.
View SolutionParallel monochromatic beam is falling normally on two slits S1 and S2 separated by d as shown in figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S1S2 and S3S4. When z=Dλ2d, the intensity measured at P is I. and when z is equal to 4Dλd, Intensity is xl. Find x.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (2), its distance from the double slits is nearly
 A30 cmB20 cmC38 cmDnone of these
A30 cmB20 cmC38 cmDnone of these - Question 2 - Select One
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. When the screen is at position (1), phase difference of waves from S1 and S2 at point P is effectively.
 A90∘B120∘C150∘D60∘
A90∘B120∘C150∘D60∘ - Question 3 - Select One
In Young's interfernce experiment has a set up as shown in figure, consider that a source of monochromatic light of wavelength 5000Å is placed at S.S1 and S2 are equidistant from S and have equal widths. A wvefront, eit light waves, which superimpose to result in an interference pattern on the screen kept at position (1). this is an experiment where coherent sources are obtained by division of wavefront. O is a point on the screen equidistant from S1andS2. P is a point on the screen 1 mm from O at which path difference between waves from S1andS2 is 11250Å. Position of amy point on the screen can be expressed by θ. The path difference is zero at O and a central bright fringe of intensity I0 is obtained at O. Q is another point 2 mm from O. If the screen is now shifted to a new position (2) [not shown in figure] so that D changes, the fringe width is found to be 50% more than its earlier value and the angular fringe width is 190 radian. Answer the following question [assume D to be large and θ very small so taht sin≈tanθ≈θ]
Q. Distance d between S1andS2 is
 A0.2 mmB45μmC20μmDnone of these
A0.2 mmB45μmC20μmDnone of these
Coherent light is incident on two fine parallel slits S1 and S2 as show in fig. If a dark fringe occurs at P, which of the following gives possible phase difference for the light waves arriving at P from S1 and S2 ?
 View Solution
View SolutionIn an interference experiment , two parallel verticals slits S1 and S2 are used. A thin glass plate is introduced in the path of light from S1. Then
View SolutionIn a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:

If a liquid is filled between the slit and the source S, what is the phase difference?View SolutionIn a modified Young's double-slit experiment, source S is kept in front of slit S1 as shown in the following figure. Find the phase difference at a point that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations:
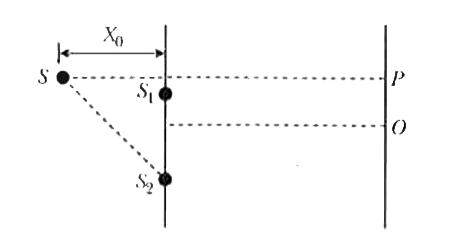
If a liquid of refractive index n is filled between the screen and slits, what is the phase difference?View SolutionAmong two interfering sources, let S1 be ahead of the phase by 90∘ relative to S2 . If an observation point P is such that PS1−PS2=1.5λ , the phase difference between the waves from S1andS2 reaching P is
View Solution

