The difference in potential of two points lying on the axis a distance of 50 cm and 100 cm respectivelym from its centre is
9×107J/Am
8×10−7J/Am
9×10−7J/Am
8×107J/Am
The correct Answer is:C
To solve the problem of finding the difference in potential (V) between two points on the axis of a magnetic dipole, we can follow these steps:
Step 1: Understand the Formula for Potential
The potential (V) at a distance r from a magnetic dipole is given by the formula:
V=μ04π⋅mcosθr2
where:
- μ0 is the permeability of free space,
- m is the magnetic moment,
- θ is the angle between the dipole moment and the line joining the dipole to the point (for points along the axis, θ=0 and cosθ=1),
- r is the distance from the center of the dipole.
Step 2: Identify the Distances
We have two points:
- Point 1 at r1=50cm=0.5m
- Point 2 at r2=100cm=1.0m
Step 3: Calculate the Potentials at Both Points
Using the formula for potential, we can calculate V1 and V2:
V1=μ04π⋅m⋅1(0.5)2
V2=μ04π⋅m⋅1(1.0)2
Step 4: Find the Difference in Potential
The difference in potential ΔV is given by:
ΔV=V1−V2=(μ04π⋅m(0.5)2)−(μ04π⋅m(1.0)2)
Factoring out the common terms:
ΔV=μ04π⋅m(1(0.5)2−1(1.0)2)
Step 5: Substitute the Values
Given:
- μ0=10−7T m/A
- m=3A m2
Now substituting the values:
ΔV=10−74π⋅3(10.25−1)
Calculating the terms:
ΔV=10−74π⋅3(4−1)=10−74π⋅3⋅3
ΔV=9×10−74π
Step 6: Calculate the Final Value
Using π≈3.14:
ΔV≈9×10−712.56≈7.16×10−8J/A
Final Answer
The difference in potential between the two points is approximately 7.16×10−8J/A.
The potential (V) at a distance r from a magnetic dipole is given by the formula:
V=μ04π⋅mcosθr2
where:
- μ0 is the permeability of free space,
- m is the magnetic moment,
- θ is the angle between the dipole moment and the line joining the dipole to the point (for points along the axis, θ=0 and cosθ=1),
- r is the distance from the center of the dipole.
We have two points:
- Point 1 at r1=50cm=0.5m
- Point 2 at r2=100cm=1.0m
Using the formula for potential, we can calculate V1 and V2:
V1=μ04π⋅m⋅1(0.5)2
V2=μ04π⋅m⋅1(1.0)2
The difference in potential ΔV is given by:
ΔV=V1−V2=(μ04π⋅m(0.5)2)−(μ04π⋅m(1.0)2)
Factoring out the common terms:
ΔV=μ04π⋅m(1(0.5)2−1(1.0)2)
Given:
- μ0=10−7T m/A
- m=3A m2
ΔV=10−74π⋅3(10.25−1)
Calculating the terms:
ΔV=10−74π⋅3(4−1)=10−74π⋅3⋅3
ΔV=9×10−74π
Using π≈3.14:
ΔV≈9×10−712.56≈7.16×10−8J/A
The difference in potential between the two points is approximately 7.16×10−8J/A.
Topper's Solved these Questions
Similar Questions
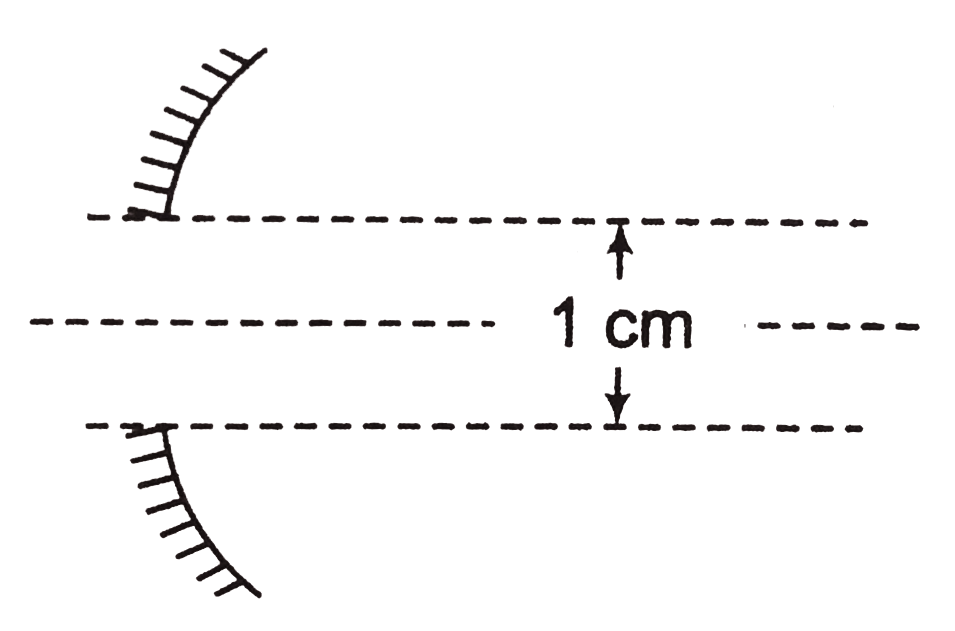
Concave mirror forms the real image of a point source lying on the optical axis at a distance of 50 cm from the mirror. The focal length of the mirror is 25 cm. The mirror is cut into and its halves are drawn a distance of 1 cm apart in a direction perpendicular to the optical axis. How will the image formed by the halves of the mirror be arranged?
 View Solution
View SolutionThe magnetic scalar potential due to a magnetic dipole at a point on its axis situated at a distance of 20cm from its centre is found to be 1.2×10−5Tm. Find the magnetic moment of the dipole.
View Solution
Knowledge Check
- Question 1 - Select One
The distance of two points on the axis of a magnet from its centre is 10cm and 20cm repectively. The ratio of magnatic intensity at these points is 12.5:1. The length of the megnet will be
A5cmB25cmC10cmD20cm - Question 2 - Select One
The potential gradient along the length of a uniform wire is 5 V/m. There are two points on the same wire at a distance of 20 cm and 40 cm from initial end of the wire. The potential difference between these points is
A1VB2VC3VD4V - Question 3 - Select One
A uniform bar RS weighs 100 g and is 80 cm long. From the end R, two masses 50 g and 100 g are hung from the bar at a distance of 10 cm and 60 cm respectively. If the bar is to remain horizontal when balanced on a knifeedge, its position is
A42 cm from SB38 cm from RC38 cm from GD42 cm from R
A uniformly charged insulating disc of radius 40 cm has charge per unit area 4.0nCm2 .The electric potential on the axis of the disc at a distance of 30 cm from its centre will be nearly
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View SolutionThe potential at a point at a distance of 25 cm from the centre of a magnetic dipole on a line inclined at angle at 60∘ with its dipole moment vector is greater than the potential at a point on the same line at a distance of 50 cm from the centre,by 3×10−7J/Am.The magnetic moment of the magnet is
View SolutionA 6 V battery is connected to the terminals of a 3 m long wire of uniform thickness and resistance of 100Ω. The difference of potential between two points on the wire separated by a distance of 50 cm will be
View SolutionThe magnetic field due to a current carrying circular loop of radius 6 cm at a point on the axis at a distance of 8 cm from the centre is 108 μT. What will be its value at the centre of the loop?
View Solution

