Prove that the locus of the point of intersection of the lines √3x−y−4√3k=0 and √3kx+ky−4√3=0 for differenet values of k is a hyperbola whose eccentericity is 2.Solution in Bengali
Step by step video & image solution for Prove that the locus of the point of intersection of the lines sqrt(3)x - y - 4 sqrt(3)k = 0 and sqrt(3)kx + ky - 4sqrt(3) = 0 for differenet values of k is a hyperbola whose eccentericity is 2. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - MULTIPLE CHOICE TYPE QUESTIONS20videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHOT ANSWER TYPE QUESTIONS16videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)7videos
DIAGRAMMATIC REPRESENTATION OF DATA
- BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams20videos
MATHEMATICAL INDUCTION
Similar Questions
If e is the eccentricity of the hyperbola x2a2−y2b2=1 , then e =
03:35View SolutionExplain what geometrical diagrams are represented by the equatio x2a2+y2a2(1−e2)=1, where a and e are constants.
03:05View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
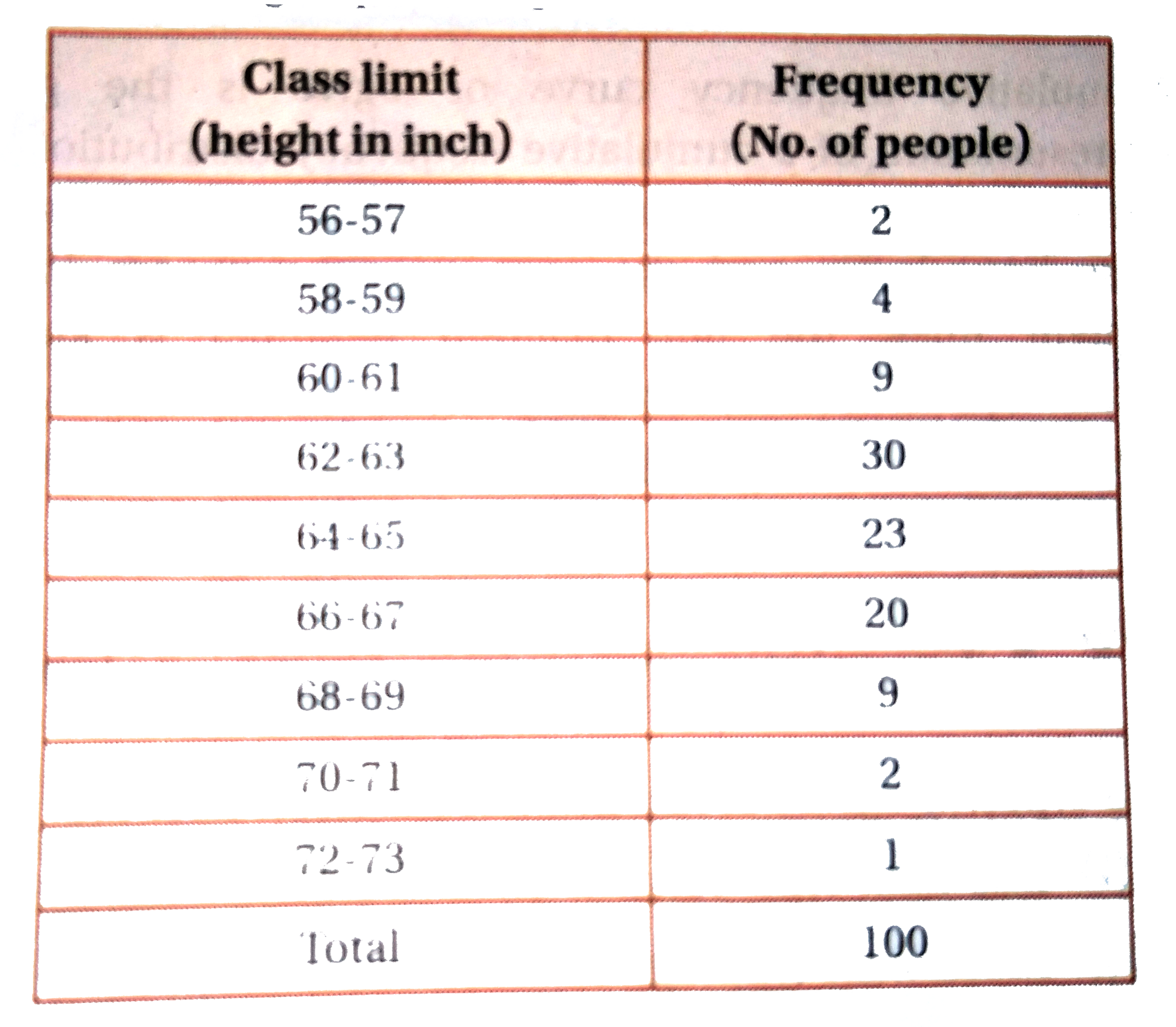Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches. 02:13View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
05:36View SolutionFind the locus of the point of intersection of the lines √3x−y−4√3t=0and√3tx+ty−4√3=0 for different values of λ.
03:58View SolutionThe locus of the point of intersection of the lines sqrt(3)x-y-4sqrt(3)t=0&sqrt(3)tx+ty-4sqrt(3)=0 (where t is a parameter) is a hyperbola whose eccentricity is:
07:38View SolutionIf y4=k+2and√√√y=4√4√4√3y4+4;k∈ real then the value of |k−2| is
02:49View SolutionThe locus of the point of intersection of the lines √3x−y−4√3λ=0 and √3λx+λy−4√3=0 is a hyperbola of eccentricity
a.1
b. 2
c. 3
d. 403:32View SolutionIf the area enclosed between the curves y=kx2 and x=ky2, where k>0, is 1 square unit. Then k is: (a) 1√3 (b) √32 (c) 2√3 (d) √3
07:02View SolutionAn equilateral triangle whose two vertices are (−2,0)and(2,0) and which lies in the first and second quadrants only is circumscribed by a circle whose equation is : (B) √3x2+√3y2−4x−4√3y=0 (C) √3x2+√3y2−4y+4√3y=0 (D) √3x2+√3y2−4y−4√3=0
03:04View SolutionThe locus of the point of intersection of lines √3x−y−4√3k=0 and √3kx+ky−4√3=0 for different value of k is a hyperbola whose eccentricity is 2.
05:26View SolutionThe locus of the point of intersection of the lines √3x−y−4√3k=0and kx√3+ky−4√3=0 is a hyperbola of eccentricity
04:25View SolutionThe locus of the point of intersection of the lines, √2x−y+4√2k=0 and √2kx+ky−4√2=0 (k is any non-zero real parameter), is:
02:29View SolutionLine sqrt(3)x-y-4sqrt(3)t=0 And sqrt(3)tx+ty-4sqrt(3)=0 (where, t Is a parameter) is the hyperbola of the intersection point of
04:55View SolutionThe locus of the point of intersection of lines √3x−y−4√3k=0 and √3kx+ky−4√3=0 for different value of k is a hyperbola whose eccentricity is 2.
03:16View SolutionThe locus of the point of intersection of the lines √3x−y−4√3λ=0 and √3λx+λy−4√3=0 is a hyperbola of eccentricity a.1 b. 2 c. 3 d. 4
03:20View Solution