AB and CD are the chords of the parabola which intersect at a point E on the axis. The radical axis of the two circles described on ABand CD as diameter always passes through
Step by step video & image solution for AB and CD are the chords of the parabola which intersect at a point E on the axis. The radical axis of the two circles described on ABand CD as diameter always passes through by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
LOL' and MOM' are two chords of parabola y2=4ax with vertex A passing through a point O on its axis. Prove that the radical axis of the circles described on LL' and MM' as diameters passes though the vertex of the parabola.
View SolutionLOL' and MOM' are two chords of parabola y2=4ax with vertex A passing through a point O on its axis. Prove that the radical axis of the circles described on LL' and MM' as diameters passes though the vertex of the parabola.
View Solution
Knowledge Check
Observe the following facts for a parabola.
(i) Axis of the parabola is the only line which can be the perpendicular bisector of the two chords of the parabola.
(ii) If AB and CD are two parallel chords of the parabola and the normals at A and B intersect at P and the normals at C and D intersect at Q, then PQ is a normal to the parabola.
For the parabola y2=4x, AB and CD are any two parallel chords having slope 1. C1 is a circle passing through O, A and B and C2 is a circle passing through O, C and D. C1andC2 intersect atA(4, -4)B(-4, 4)C(4, 4)D(-4, -4)
AB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
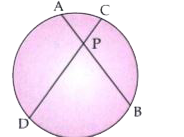
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionIn Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP=CP. Show that AB=CD
View SolutionIf AB and CD are two chords of a circle and AB>CD, then the chord which is nearer to the center is……………………
View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View Solution
