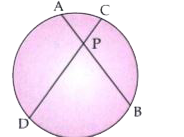
AB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM AB and ON CD, show that OMPN is a square.
To show that OMPN is a square, we will follow these steps:
Step 1: Understand the Given Information
We have two equal chords AB and CD of a circle with center O. These chords intersect at point P at right angles. We also know that OM is perpendicular to AB and ON is perpendicular to CD.
Step 2: Establish Right Angles
Since OM is perpendicular to AB and ON is perpendicular to CD, we can conclude that:
- Angle OMP = 90 degrees
- Angle ONP = 90 degrees
- Angle PMN = 90 degrees
- Angle PNQ = 90 degrees
Thus, all angles in quadrilateral OMPN are right angles.
Hint: Remember that if all angles in a quadrilateral are right angles, it is a rectangle.
Step 3: Use the Property of Chords
Since OM is perpendicular to chord AB, it bisects AB. Therefore, let PM = MB = x (where x is half the length of chord AB). Similarly, since ON is perpendicular to chord CD, it bisects CD. Let PN = ND = y (where y is half the length of chord CD).
Hint: The perpendicular from the center of a circle to a chord bisects the chord.
Step 4: Equal Lengths of Chords
Since AB and CD are equal chords, we have:
- AB = CD
- Therefore, PM + MB = PN + ND
- This implies 2x = 2y, or x = y.
Hint: Equal chords in a circle imply that their perpendicular bisectors are equal.
Step 5: Establish the Lengths of the Sides
Since we have established that PM = PN (let's denote this common length as 'a'), we can conclude:
- MP = PN = a
- OM = ON = a
Step 6: Show that OMPN is a Square
Since OMPN has all right angles and all sides are equal (OM = MP = PN = ON = a), we can conclude that OMPN is a square.
Hint: A quadrilateral with equal sides and right angles is a square.
Conclusion
Thus, we have shown that OMPN is a square.
We have two equal chords AB and CD of a circle with center O. These chords intersect at point P at right angles. We also know that OM is perpendicular to AB and ON is perpendicular to CD.
Since OM is perpendicular to AB and ON is perpendicular to CD, we can conclude that:
- Angle OMP = 90 degrees
- Angle ONP = 90 degrees
- Angle PMN = 90 degrees
- Angle PNQ = 90 degrees
Since OM is perpendicular to chord AB, it bisects AB. Therefore, let PM = MB = x (where x is half the length of chord AB). Similarly, since ON is perpendicular to chord CD, it bisects CD. Let PN = ND = y (where y is half the length of chord CD).
Since AB and CD are equal chords, we have:
- AB = CD
- Therefore, PM + MB = PN + ND
- This implies 2x = 2y, or x = y.
Since we have established that PM = PN (let's denote this common length as 'a'), we can conclude:
- MP = PN = a
- OM = ON = a
Since OMPN has all right angles and all sides are equal (OM = MP = PN = ON = a), we can conclude that OMPN is a square.
Thus, we have shown that OMPN is a square.
Topper's Solved these Questions
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(C)
Explore 29 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(A)
Explore 14 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:DISTANCE FORMULA
Explore 11 Videos
- CIRCLES Book:ICSEChapter:CIRCLES Exercise:TOPIC-2
Explore 25 Videos
Similar Questions
AB and CD are two equal chords of a circle with centre O which intersect each other at right angle at P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ=150∘ find angleAPQ
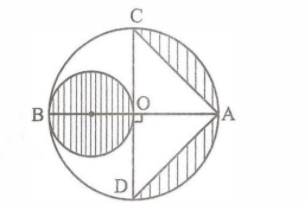
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View Solution